题目内容
计算出数列1,1+2+1,1+2+3+2+1,…,1+2+3+…+n+…+3+2+1,…的前n项,并猜想出数列的通项公式,然后用数学归纳法证明.
解:计算并观察得:1=12,1+2+1=4=22,1+2+3+2+1=9=32,
由此可猜想得1+2+3+…+n+…+3+2+1=n2,
故an=n2,
下面用数学归纳法证明:
(1)当n=1时,a1=1=12,猜想正确.
(2)假设n=k时猜想正确,即
ak=1+2+3+…+k+…+3+2+1=k2,那么
ak+1=1+2+3+…+k+(k+1)+k+…+3+2+1
=(1+2+3+…+k+…+3+2+1)+(k+1)+k
=k2+(k+1)+k
=(k+1)2,
∴n=k+1时猜想正确.
由(1)(2)可知1+2+3+…+n+…+3+2+1=n2对任意正整数均成立.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
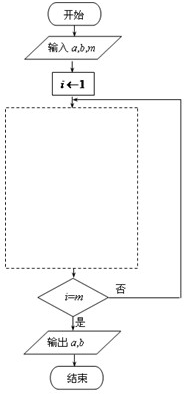 若数列{an},{bn}中,a1=a,b1=b,
若数列{an},{bn}中,a1=a,b1=b,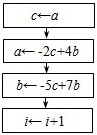 B、
B、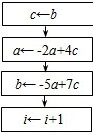
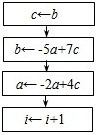 D、
D、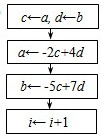
 (m∈N*).
(m∈N*). ,记
,记 (n∈N*),求数列{an}的通项公式;
(n∈N*),求数列{an}的通项公式; (m∈N*).
(m∈N*).