题目内容
根据定义在集合A上的函数y=f(x),构造一个数列发生器,其工作原理如下:①输入数据x0∈A,计算出x1=f(x0);②若x1∉A,则数列发生器结束工作;若x1∈A,则输出x1,并将x1反馈回输入端,再计算出x2=f(x1),并依此规律继续下去.若集合A={x|0<x<1}},f(x)=
(m∈N*).
(理)(1)求证:对任意x0∈A,此数列发生器都可以产生一个无穷数列{xn};
(2)若x0=
,记an=
(n∈N*),求数列{an}的通项公式;
(3)在(2)的条件下,证明:3≤am<4(n∈N*).
(文)(1)求证:对任意x0∈A,此数列发生器都可以产生一个无穷数列{xn};
(2)若m=1,求证:数列{xn}单调递减;
(3)若x0=
,记an=
(n∈N*),求数列{an}的通项公式.
| mx |
| m+1-x |
(理)(1)求证:对任意x0∈A,此数列发生器都可以产生一个无穷数列{xn};
(2)若x0=
| 1 |
| 2 |
| 1 |
| xn |
(3)在(2)的条件下,证明:3≤am<4(n∈N*).
(文)(1)求证:对任意x0∈A,此数列发生器都可以产生一个无穷数列{xn};
(2)若m=1,求证:数列{xn}单调递减;
(3)若x0=
| 1 |
| 2 |
| 1 |
| xn |
分析:(理科)(1)当x∈A,即0<x<1 时,由m∈N*,可知0<f(x)<1,即f(x)∈A,故对任意x0∈A,有x1=f(x0)∈A,由 x1∈A 有x2=f(x1)∈A,以此类推,可一直继续下去,从而可以产生一个无穷数列;
(2)易证{bn}是以
为首项,以
为公比的等比数列,从而求出bn=(
)n,从而求出an=(
)n+1;
(3)要证3≤(
)m+1<4,只需证2≤(1+
)m<3,当m∈N*时,利用二项式定理以及放缩法证明不等式即可.
(文科)(1)同理科(1);
(2)m=1时,f(x)=
(0<x<1),依题意,
=
-1⇒
-1=2(
-1)⇒{
-1}是以
-1=2为首项,2为公比的等比数列,从而可求数列{
-1}的通项公式,即可可证数列{xn}单调递减;
(3)同理科(2).
(2)易证{bn}是以
| m+1 |
| m |
| m+1 |
| m |
| m+1 |
| m |
| m+1 |
| m |
(3)要证3≤(
| m+1 |
| m |
| 1 |
| m |
(文科)(1)同理科(1);
(2)m=1时,f(x)=
| x |
| 2-x |
| 1 |
| xn+1 |
| 2 |
| xn |
| 1 |
| xn+1 |
| 1 |
| xn |
| 1 |
| xn |
| 1 |
| x1 |
| 1 |
| xn |
(3)同理科(2).
解答:解:(1)当x∈A,即0<x<1 时,由m∈N*,可知m+1-x>0,
∴
>0,又
-1=
<0,
∴
<1,
∴0<f(x)<1,即f(x)∈A
故对任意x0∈A,有x1=f(x0)∈A,
由 x1∈A 有x2=f(x1)∈A,
x2∈A 有x3=f(x2)∈A;
以此类推,可一直继续下去,从而可以产生一个无穷数列
(2)由xn+1=f(xn)=
,可得
=
•
-
,
∴an+1=
an-
,即an+1-1=
(an-1).
令bn=an-1,则bn+1=
bn,又b1=
,
所以{bn}是以
为首项,以
为公比的等比数列.
∴bn=(
)n,即an=(
)n+1,即an=bn+1.
(3)要证3≤am=(
)m+1<4,只需证2≤(1+
)m<3,当m∈N*时,
有(1+
)m=
•(
)0+
•(
)1+…+
•(
)m≥2,
∵当k≥2时,
•(
)k=
•(
)k<
≤
-
,
∴当k≥2时,(1+
)m=
•(
)0+
•(
)1+…+
•(
)m
<1+1+(1-
)+(
-
)+…+(
-
)
=3-
<3.
又当m=1时,2≤(1+
)1=2<3,
∴对任意的n∈N*,都有2≤(1+
)m<3,
∴对于任意m∈N*,3≤am<4.
文科(1)同理科(1)略;
(2)m=1时,f(x)=
(0<x<1),
依题意,xn+1=
=
,
∴
=
-1,
∴
-1=2(
-1),又x1=
=
,
∴
-1=
-2>0,
∴数列{
-1}是以
-2为首项,2为公比的等比数列,
∴
-1=(
-2)•2n-1,
∴
=(
-2)•2n-1+1,显然数列{
}为正项递增数列,
∴数列{xn}为递减数列.
(3)同理科(2).
∴
| mx |
| m+1-x |
| mx |
| m+1-x |
| (m+1)(x-1) |
| m+1-x |
∴
| mx |
| m+1-x |
∴0<f(x)<1,即f(x)∈A
故对任意x0∈A,有x1=f(x0)∈A,
由 x1∈A 有x2=f(x1)∈A,
x2∈A 有x3=f(x2)∈A;
以此类推,可一直继续下去,从而可以产生一个无穷数列
(2)由xn+1=f(xn)=
| mxn |
| m+1-xn |
| 1 |
| xn+1 |
| m+1 |
| m |
| 1 |
| x |
| 1 |
| m |
∴an+1=
| m+1 |
| m |
| 1 |
| m |
| m+1 |
| m |
令bn=an-1,则bn+1=
| m+1 |
| m |
| m+1 |
| m |
所以{bn}是以
| m+1 |
| m |
| m+1 |
| m |
∴bn=(
| m+1 |
| m |
| m+1 |
| m |
(3)要证3≤am=(
| m+1 |
| m |
| 1 |
| m |
有(1+
| 1 |
| m |
| C | 0 m |
| 1 |
| m |
| C | 1 m |
| 1 |
| m |
| C | m m |
| 1 |
| m |
∵当k≥2时,
| C | k m |
| 1 |
| m |
| m(m-1)…(m-k+1) |
| k! |
| 1 |
| m |
| 1 |
| k! |
| 1 |
| k-1 |
| 1 |
| k |
∴当k≥2时,(1+
| 1 |
| m |
| C | 0 m |
| 1 |
| m |
| C | 1 m |
| 1 |
| m |
| C | m m |
| 1 |
| m |
<1+1+(1-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n-1 |
| 1 |
| n |
=3-
| 1 |
| n |
又当m=1时,2≤(1+
| 1 |
| 1 |
∴对任意的n∈N*,都有2≤(1+
| 1 |
| m |
∴对于任意m∈N*,3≤am<4.
文科(1)同理科(1)略;
(2)m=1时,f(x)=
| x |
| 2-x |
依题意,xn+1=
| mxn |
| m+1-xn |
| xn |
| 2-xn |
∴
| 1 |
| xn+1 |
| 2 |
| xn |
∴
| 1 |
| xn+1 |
| 1 |
| xn |
| mx0 |
| m+1-x0 |
| x0 |
| 2-x0 |
∴
| 1 |
| xn |
| 2 |
| x0 |
∴数列{
| 1 |
| xn |
| 2 |
| x0 |
∴
| 1 |
| xn |
| 2 |
| x0 |
∴
| 1 |
| xn |
| 2 |
| x0 |
| 1 |
| xn |
∴数列{xn}为递减数列.
(3)同理科(2).
点评:本题主要考查了等比数列的通项公式,以及无穷数列的证明和二项式定理证明不等式,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
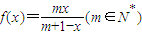
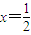 ,记
,记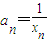 (n∈N*),求数列{an}的通项公式.
(n∈N*),求数列{an}的通项公式.