题目内容
【题目】如图，四棱锥
中，
平面
，
，
，
，
为
的中点，
与
相交于点
.
（Ⅰ）求证：
平面
；
（Ⅱ）求直线
与平面
所成角的正弦值.
【答案】（Ⅰ）详见解析；（Ⅱ）
.
【解析】
（Ⅰ）先证明
面
得到
，再证明
得到
平面
.
（Ⅱ）以
为原点，分别以
为
轴，
轴，
轴的建立直角坐标系.计算平面
的法向量为
，再利用向量夹角公式得到答案.
解：（Ⅰ）
由已知
平面
，可得
，
，
由题意得，为直角梯形，如图所示，
，所以
为平行四边形，
所以
，所以
.
又因为
，且
，
所以面，
故.
在直角梯形中，
，
因为面，所以，
所以
为等腰直角三角形，为斜边
上的中点，
所以.且
，
所以平面
（Ⅱ）法一：以为原点，分别以为轴，轴，轴的建立直角坐标系.
不妨设
，
，
，
，
设
是平面的法向量.
满足
，
所以
，
则令
，解得
法二：（等体积法求
到平面的距离）
设
，计算可得
，
，
，
，
解得
【题目】某地区2007年至2013年农村居民家庭纯收入y（单位：千元）的数据如下表：
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
（1）求y关于t的线性回归方程；
（2）利用（1）中的回归方程，分析2007年至2013年该地区农村居民家庭人均纯收入的变化情况，并预测该地区2015年农村居民家庭人均纯收入.
附：回归直线的斜率和截距的最小二乘法估计公式分别为：
，
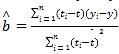【题目】某机构为调查我国公民对申办奥运会的态度，选了某小区的100位居民调查结果统计如下：
支持 | 不支持 | 合计 | |
年龄不大于50岁 | 80 | ||
年龄大于50岁 | 10 | ||
合计 | 70 | 100 |
（1）根据已有数据，把表格数据填写完整；
（2）能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关？
（3）已知在被调查的年龄大于50岁的支持者中有5名女性，其中2位是女教师，现从这5名女性中随机抽取3人，求至多有1位女教师的概率.
附：
，
| 0.100 | 0.050 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
