题目内容
【题目】已知在平面直角坐标系中，动点P到定点F(1,0)的距离比到定直线x=-2的距离小1.
（1）求动点P的轨迹C的方程；
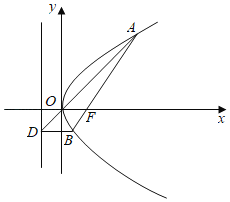
（2）若直线l与（1）中轨迹C交于A，B两点，通过A和原点O的直线交直线x=-1于D，求证：直线DB平行于x轴.
【答案】（1）
；（2）证明见解析.
【解析】
（1）判断轨迹为抛物线，转化求解抛物线方程即可．
（2）画出图形，设直线
的方程为
代入抛物线方程，设
，
，
，
，取得
的纵坐标，然后推出结果．
（1）解：动点
到
的距离比到定直线
的距离小
，则与到定直线
的距离相等，根据抛物线的定义可知，所求轨迹为以为焦点，直线为准线的抛物线，其方程为①
（2）证明：设直线的方程为②
②代入①，整理得
，
设，，，，则
，
所以点
的纵坐标
③
因为
，所以直线
的方程为
④
可得
的纵坐标为
⑤
由③⑤知，
轴．
练习册系列答案
相关题目
【题目】微信是现代生活中进行信息交流的重要工具.据统计，某公司200名员工中
的人使用微信，其中每天使用微信时间少于一小时的有60人，其余的员工每天使用微信时间不少于一小时，若将员工分成青年（年龄小于40岁）和中年（年龄不小于40岁）两个阶段，那么使用微信的人中
是青年人.若规定：每天使用微信时间不少于一小时为经常使用微信，那么经常使用微信的员工中
都是青年人.
（1）若要调查该公司使用微信的员工经常使用微信与年龄的关系，完成
列联表：
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
（2）由列联表中所得数据判断，能否在犯错误的概率不超过
的前提下认为“经常使用微信与年龄有关”？
| 0.010 | 0.001 |
| 6.635 | 10.828 |
