题目内容
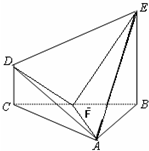 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=| π | 2 |
(1)设平面ABE与平面ACD的交线为直线l,求证:l∥平面BCDE;
(2)设F是BC的中点,求证:平面AFD⊥平面AFE;
(3)求几何体ABCDE的体积.
分析:(1)根据DC⊥平面ABC,EB⊥平面ABC判断出DC∥EB,进而利用直线与平面平行的判断定理可知DC∥平面ABE,利用直线与平面平行的性质可推断出DC∥l,进而可推断出l∥平面BCDE.
(2)根据DC⊥平面ABC推断出DC⊥AF,同时利用AB=AC,F是BC的中点推断出AF⊥BC,AF⊥平面BCDE进而利用直线与平面垂直的性质可知AF⊥DF,AF⊥EF进而可推断出∠DFE是面AFD和面AFE所成二面角的平面角,利用勾股定理可推断出FD⊥FE,推断出∠DFE=90°,进而证明出平面AFD⊥平面AFE.
(3)几何体ABCDE的体积,即四棱锥A-BCDE的体积,其底面是一个直角梯形,高为AF,代入体积公式可得答案.
(2)根据DC⊥平面ABC推断出DC⊥AF,同时利用AB=AC,F是BC的中点推断出AF⊥BC,AF⊥平面BCDE进而利用直线与平面垂直的性质可知AF⊥DF,AF⊥EF进而可推断出∠DFE是面AFD和面AFE所成二面角的平面角,利用勾股定理可推断出FD⊥FE,推断出∠DFE=90°,进而证明出平面AFD⊥平面AFE.
(3)几何体ABCDE的体积,即四棱锥A-BCDE的体积,其底面是一个直角梯形,高为AF,代入体积公式可得答案.
解答:证明:(1)∵DC⊥平面ABC,EB⊥平面ABC
∴DC∥BE,
∴DC∥平面ABE
又l=平面ACD∩平面ABE
∴DC∥l
又l?平面BCDE,DC?平面BCDE
∴l∥平面BCDE.
(2)∵DC⊥平面ABC
∴DC⊥AF
∵AB=AC,F是BC的中点
∴AF⊥BC,AF⊥平面BCDE
∴AF⊥DF,AF⊥EF
∴∠DFE是面AFD和面AFE所成二面角的平面角
在△DEF中,FD=
,FE=
,DE=3
FD⊥FE,即∠DFE=90°
∴平面AFD⊥平面AFE
(3)几何体ABCDE的体积V=VA-BCDE=
•SBCDE•AF=
×
(1+2)×2
×
=2
∴DC∥BE,
∴DC∥平面ABE
又l=平面ACD∩平面ABE
∴DC∥l
又l?平面BCDE,DC?平面BCDE
∴l∥平面BCDE.
(2)∵DC⊥平面ABC
∴DC⊥AF
∵AB=AC,F是BC的中点
∴AF⊥BC,AF⊥平面BCDE
∴AF⊥DF,AF⊥EF
∴∠DFE是面AFD和面AFE所成二面角的平面角
在△DEF中,FD=
| 3 |
| 6 |
FD⊥FE,即∠DFE=90°
∴平面AFD⊥平面AFE
(3)几何体ABCDE的体积V=VA-BCDE=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:本题主要考查了平面与平面垂直的性质,直线与平面平行的判定等.要求考生对基本定理能熟练掌握.

练习册系列答案
相关题目
 如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点.
如图,在几何体ABCDE中,△ABC是等腰直角三角形,∠ABC=90°,BE和CD都垂直于平面ABC,且BE=AB=2,CD=1,点F是AE的中点. 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC= 在几何体ABCDE中,∠BAC=
在几何体ABCDE中,∠BAC=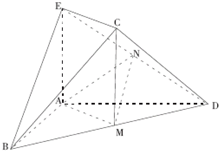 (2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=
(2013•合肥二模)如图,在几何体ABCDE中,AB=AD=2,AB丄AD,AD丄平面ABE.M为线段BD的中点,MC∥AE,AE=MC=