题目内容
10．在四面体ABCD中，已知AD⊥BC，AD=6，BC=2，且$\frac{AB}{BD}$=$\frac{AC}{CD}$=2，则V四面体ABCD的最大值为（ ）| A． | 6 | B． | 2$\sqrt{11}$ | C． | 2$\sqrt{15}$ | D． | 8 |
分析 作BE⊥AD于E，连接CE，取BC中点F，推出四面体ABCD的体积的最大值，当△ABD是等腰三角形时几何体的体积最大，求解即可．
解答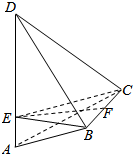 
解：作BE⊥AD于E，连接CE，则AD⊥平面BEC，所以CE⊥AD，
取BC中点F，所以EF⊥BC，EF⊥AD，四面体ABCD的体积的最大值，只需EF最大即可，即需BE最大，
以AD所在直线为x轴，AD的垂直平分线为y轴，则A（-3，0），D（3，0），
设B（x，y），则∵$\frac{AB}{BD}$=2，
∴AB=2BD，
∴（x+3）2+y2=4（x-3）2+4y2，
∴（x-5）2+y2=16，
∴BE最大为4，此时CE=4，$\frac{AC}{CD}$=2．
∴EF=$\sqrt{16-1}$=$\sqrt{15}$，
故四面体ABCD的体积的最大值为$\frac{1}{3}×\frac{1}{2}×2×\sqrt{15}×6$=2$\sqrt{15}$
故选：C．
点评 本题考查棱柱、棱锥、棱台的体积，考查空间想象能力，逻辑推理能力以及计算能力．
练习册系列答案
相关题目
如图，已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{1}{2}$，点A（0，$\sqrt{3}$）和点P都在椭圆C1上，椭圆C2方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=4．
15．椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1（{a＞b＞0}）$的两焦点为F1（-c，0）、F2（c，0），P为直线$x=\frac{a^2}{c}$上一点，F1P的垂直平分线恰过F2点，则e的取值范围为（ ）
| A． | $（{0，\frac{{\sqrt{3}}}{3}}）$ | B． | $（{0，\frac{{\sqrt{3}}}{3}}]$ | C． | $（{\frac{{\sqrt{3}}}{3}，1}）$ | D． | $[{\frac{{\sqrt{3}}}{3}，1}）$ |
2．设全集U={0，1，2，3，4}，集合A={1，2，3}，B={2，3，4}，则A∪（∁∪B）=（ ）
| A． | {0，1，2，3} | B． | {1} | C． | {0，1} | D． | {0} |
19．已知函数f（x）=ex-x2（x＜0）与g（x）=x2-ln（a-x）的图象上存在关于x轴的对称点，则a的取值范围为（ ）
| A． | （-∞，e） | B． | $（{-∞，\frac{1}{e}}）$ | C． | （-∞，2e） | D． | $（{-∞，\frac{1}{2e}}）$ |