题目内容
 如图,AC为⊙O的直径,弦BD⊥AC于点P,PC=2,PA=8,则cos∠ACB的值为
如图,AC为⊙O的直径,弦BD⊥AC于点P,PC=2,PA=8,则cos∠ACB的值为
分析:本题考查的知识点是与圆相关的比例线段,由AC为⊙O的直径,弦BD⊥AC于点P,根据射影定理,结合PC=2,PA=8,我们可以求出CD的长,解三角形CDP,即可求出cos∠ACB的值.
解答:解:由射影定理得CD2=CP•CA=2×10,
∴CD=2
,
则cos∠ACB
=sin∠A
=sin∠D
=
=
=
.
故答案为:
∴CD=2
| 5 |
则cos∠ACB
=sin∠A
=sin∠D
=
| CP |
| CD |
| 2 | ||
2
|
| ||
| 5 |
故答案为:
| ||
| 5 |
点评:当出现有双垂直情况时,即在直角三角形出现有斜边上的高,我们可以利用射影定理分析边与边的关系.

练习册系列答案
相关题目
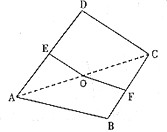 如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )
如图,点O是正方形纸片ABCD的中心,点E,F分别为AD,BC的中点,现沿对角线AC把纸片折成直二面角,则纸片折后∠EOF的大小为( )| A、30° | B、60° | C、120° | D、150° |
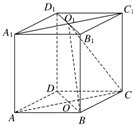 如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,则二面角O1-BC-D的大小为
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,则二面角O1-BC-D的大小为 (Ⅰ)求直三棱柱ABC-A′B′C′的体积;
(Ⅰ)求直三棱柱ABC-A′B′C′的体积; 与直线
与直线 的夹角大小为
的夹角大小为
 B.(不等式选讲)要使关于x的不等式
B.(不等式选讲)要使关于x的不等式 在实数
在实数