题目内容
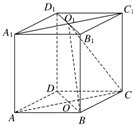 如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,则二面角O1-BC-D的大小为
如图,直四棱柱ABCD-A1B1C1D1的高为3,底面是边长为4且∠DAB=60°的菱形,AC∩BD=O,A1C1∩B1D1=O1,则二面角O1-BC-D的大小为60°
60°
.分析:作OF⊥BC,连接O1F,由O1O⊥平面ABCD及三垂线定理可得BC⊥O1F,利用二面角的定义可得∠O1FO是二面角O1-BC-D的平面角.再利用菱形的性质及含30°角的直角三角形的性质可得出OF,进而即可得出答案.
解答:解:作OF⊥BC,连接O1F,O1O.
∵O1O⊥平面ABCD,∴BC⊥O1F.
∴∠O1FO是二面角O1-BC-D的平面角.
在Rt△OBF中,∵BC=4,∠OBF=60°,
∴OF=
.
在Rt△O1OF中,tan∠O1FO=
=
=
.
∴∠O1FO=60°.
∴二面角O1-BC-D的大小为60°.
故答案为60°.

∵O1O⊥平面ABCD,∴BC⊥O1F.
∴∠O1FO是二面角O1-BC-D的平面角.
在Rt△OBF中,∵BC=4,∠OBF=60°,
∴OF=
| 3 |
在Rt△O1OF中,tan∠O1FO=
| O1O |
| OF |
| 3 | ||
|
| 3 |
∴∠O1FO=60°.
∴二面角O1-BC-D的大小为60°.
故答案为60°.
点评:熟练掌握直棱柱的性质、三垂线定理、菱形的性质、含30°角的直角三角形的性质、二面角的定义是解题的关键.

练习册系列答案
相关题目
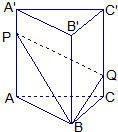 如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为
如图:直三棱柱ABC-A′B′C′的体积为V,点P、Q分别在侧棱AA′和CC′上,AP=C′Q,则四棱锥B-APQC的体积为 如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2.
如图,直三棱柱ABC-A1B1C1中,AB⊥BC,D为AC的中点,AA1=AB=2. 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是菱形,∠ABC=45°,其侧面展开图是边长为8的正方形.E、F分别是侧棱AA1、CC1上的动点,AE+CF=8. (2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点.
(2012•房山区二模)如图,直四棱柱ABCD-A1B1C1D1中,底面ABCD是菱形,且∠ABC=60°,E为棱CD的中点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.