题目内容
12.已知$\overrightarrow{a}$=(0,1),|$\overrightarrow{b}$|=4,且$\overrightarrow{a}$•$\overrightarrow{b}$=2,则向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |
分析 由$\overrightarrow{a}$=(0,1)求出$|\overrightarrow{a}|$,结合已知再由数量积求夹角公式得答案.
解答 解:∵$\overrightarrow{a}$=(0,1),∴$|\overrightarrow{a}|=1$,
又|$\overrightarrow{b}$|=4,且$\overrightarrow{a}$•$\overrightarrow{b}$=2,
∴cos$<\overrightarrow{a},\overrightarrow{b}>$=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{2}{1×4}=\frac{1}{2}$.
∴向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角为$\frac{π}{3}$.
故选:C.
点评 本题考查平面向量的数量积运算,考查向量模的求法,是基础题.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
3.在空间四边形OABC中,M为BC的中点,N为OM的中点,连接AC,则向量$\overrightarrow{AO}+\frac{1}{2}$($\overrightarrow{AB}+\overrightarrow{AC}$)化简后的结果为( )
| A. | $\overrightarrow{ON}$ | B. | $\overrightarrow{AM}$ | C. | $\overrightarrow{AN}$ | D. | 2$\overrightarrow{AN}$ |
 如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.
如图,在四边形ABCD中,AD=4,AB=5,AD⊥CD,cos∠ADB=$\frac{9}{16}$,∠DCB=135°,则BC=$\frac{27\sqrt{2}}{8}$.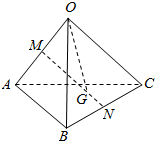 如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.
如图,在三棱锥O-ABC中,M,N分别是棱OA、CB的中点,点G在线段MN上,且MG=2GN,设$\overrightarrow{OA}$=a,$\overrightarrow{OB}$=b,$\overrightarrow{OC}$=c.