题目内容
(12分)若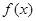 是定义在
是定义在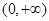 上的增函数,且对一切
上的增函数,且对一切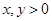 ,满足
,满足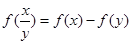 .
.
(1)求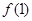 的值;
的值;
(2)若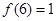 ,解不等式
,解不等式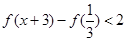
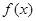 是定义在
是定义在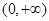 上的增函数,且对一切
上的增函数,且对一切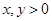 ,满足
,满足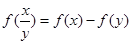 .
.(1)求
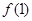 的值;
的值;(2)若
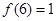 ,解不等式
,解不等式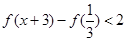
⑴  ⑵
⑵ 
 ⑵
⑵ 
试题分析:解(1)在
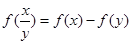 中令
中令
则有
 ∴
∴
(2)∵
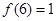 ∴
∴ ∴
∴ 即:
即: ∵
∵ 上的增函数
上的增函数∴
 解得
解得 即不等式的解集为(-3,9)
即不等式的解集为(-3,9)点评:本题已经告知函数在
 上的单调性,实质已经降低了本题的难度,本题还可不给单调性而增加条件比如:当
上的单调性,实质已经降低了本题的难度,本题还可不给单调性而增加条件比如:当 时,
时, 让学生自己证明函数在相应区间的单调性,进一步考查定义法证明函数单调性的方法
让学生自己证明函数在相应区间的单调性,进一步考查定义法证明函数单调性的方法
练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
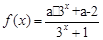 .
. 
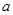 使函数f(x)为奇函数?证明你的结论;
使函数f(x)为奇函数?证明你的结论;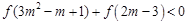 .
.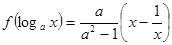
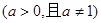
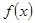 ;
;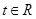 ,不等式
,不等式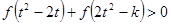 恒成立,求
恒成立,求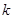 的取值范围。
的取值范围。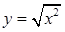 与
与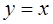
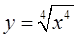 与
与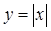
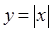 与
与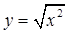 与
与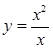
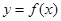 的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则
的图象是曲线OAB,其中点O、A、B的坐标分别是(0,0),(1,2),(3,1),则 的值是
的值是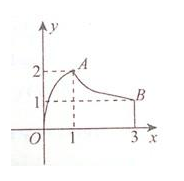

 恒成立,求m的取值范围
恒成立,求m的取值范围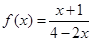 ,则
,则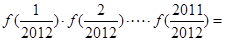 ________
________ 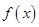 是定义在
是定义在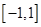 上的奇函数,且
上的奇函数,且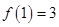 ,若
,若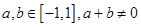 时,有
时,有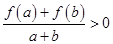 成立.
成立.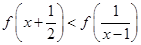 ;
;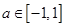 时,
时, 对所有的
对所有的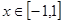 恒成立,求实数
恒成立,求实数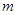 的取值范围.
的取值范围.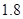 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若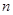 天购买一次,需要支付
天购买一次,需要支付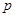 是多少元?[
是多少元?[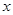 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这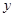 (元)关于
(元)关于