题目内容
已知函数 ,
, .
.
(Ⅰ)当 时,求函数
时,求函数 的极小值;
的极小值;
(Ⅱ)若函数 在
在 上为增函数,求
上为增函数,求 的取值范围.
的取值范围.
解:(Ⅰ)定义域 .
.
当 时,
时, ,
, .
.
令 ,得
,得 .
.
当 时,
时, ,
, 为减函数;
为减函数;
当 时,
时, ,
, 为增函数.
为增函数.
所以函数 的极小值是
的极小值是 . ……………… 5分
. ……………… 5分
(Ⅱ)由已知得 .
.
因为函数 在
在 是增函数,所以
是增函数,所以 ,对
,对 恒成立.
恒成立.
由 得
得 ,即
,即 对
对 恒成立.
恒成立.
设 ,要使“
,要使“ 对
对 恒成立”,只要
恒成立”,只要 .
.
因为 ,令
,令 得
得 .
.
当 时,
时, ,
, 为减函数;
为减函数;
当 时,
时, ,
, 为增函数.
为增函数.
所以 在
在 上的最小值是
上的最小值是 .
.
故函数 在
在 是增函数时,实数
是增函数时,实数 的取值范围是
的取值范围是 …… 13分
…… 13分

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,定义函数
,定义函数 给出下列命题:
给出下列命题: ; ②函数
; ②函数 是奇函数;③当
是奇函数;③当 时,若
时,若 ,
, ,总有
,总有 成立,其中所有正确命题的序号是
成立,其中所有正确命题的序号是 ,
, .若
.若 ∥
∥ ,则实数
,则实数 ______.
______.  ,
, ,
, ,
, ,点
,点 分别在线段
分别在线段
 上运动,且
上运动,且 ,设
,设 与
与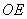 交于点
交于点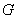 ,则点
,则点 B.
B.
 D.
D.
 满足
满足 若
若 恒成立,则实数
恒成立,则实数 的最大值是 .
的最大值是 . 是偶函数,且
是偶函数,且 则
则
 的两条渐近线为
的两条渐近线为 ,过右焦点
,过右焦点 作垂直
作垂直 的直线交
的直线交 两点.若
两点.若 成等差数列,则双曲线的离心率为
成等差数列,则双曲线的离心率为 (B)
(B) (C)
(C) (D)
(D)
 ,
, ,若
,若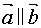 ,则代数式
,则代数式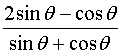 的值是 .
的值是 .