题目内容
设函数f（x）=|x-a|+|x+3|
（1）若a=2，解不等式f（x）＜7；
（2）如果?x∈R，f（x）≥2，求a的取值范围．
（1）若a=2，解不等式f（x）＜7；
（2）如果?x∈R，f（x）≥2，求a的取值范围．
考点：绝对值不等式的解法
专题：不等式的解法及应用
分析：（1）不等式即|x-2|+|x+3|＜7．根据绝对值的意义数轴上-4、3对应点到2和-3对应点的距离之和正好等于7，可得不等式的解集．
（2）由题意可得|x-a|+|x+3|≥2 恒成立，故数轴上a对应点到-3对应点的距离最小等于2 由此可得a的范围
（2）由题意可得|x-a|+|x+3|≥2 恒成立，故数轴上a对应点到-3对应点的距离最小等于2 由此可得a的范围
解答：
解：（1）∵a=2，不等式f（x）＜7 即|x-2|+|x+3|＜7．
根据绝对值的意义，|x-2|+|x+3|表示数轴上的x对应点到2和-3对应点的距离之和，
数轴上-4、3对应点到2和-3对应点的距离之和正好等于7，
故不等式的解集为 （-4，3）．
（2）∵f（x）≥2恒成立，即|x-a|+|x+3|≥2 恒成立，
故数轴上a对应点到-3对应点的距离最小等于2，∴a≤-5，或a≥-1，
即a的范围是 （-∞，-5]∪[-1，+∞）．
根据绝对值的意义，|x-2|+|x+3|表示数轴上的x对应点到2和-3对应点的距离之和，
数轴上-4、3对应点到2和-3对应点的距离之和正好等于7，
故不等式的解集为 （-4，3）．
（2）∵f（x）≥2恒成立，即|x-a|+|x+3|≥2 恒成立，
故数轴上a对应点到-3对应点的距离最小等于2，∴a≤-5，或a≥-1，
即a的范围是 （-∞，-5]∪[-1，+∞）．
点评：本题主要绝对值的意义，绝对值不等式的解法，函数的恒成立问题，
练习册系列答案
相关题目
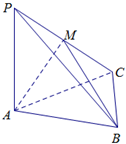如图，底面是正三角形的三棱锥P-ABC中，PA⊥底面ABC，M为PC中点，且PA=AB，其中下列四个命题：
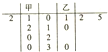2014年1月8日是传统的腊八节，大家开始购买年货，某淘宝网店趁势推出“抢红包”的促销活动，已知每人有5次抢红包的机会，每次可得1至30元不等的红包，甲、乙二人在这5次抢红包活动中获得红包金额的茎叶图如图所示，若甲5次获得红包金额的均值为