题目内容

设椭圆
x2
a2
+
y2
b2
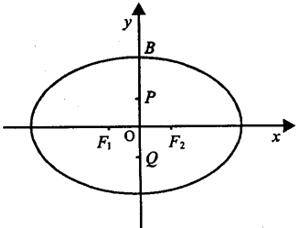
=1(a＞b＞0)的左，右两个焦点分别为F1，F2，短轴的上端点为B，短轴上的两个三等分点为P，Q，且F1PF2Q为正方形．
（1）求椭圆的离心率；
（2）若过点B作此正方形的外接圆的切线在x轴上的一个截距为-
3
2
4
，求此椭圆方程．
（1）由题意知：P(0，
b
3
)，设F1（-c，0）
因为F1PF2Q为正方形，所以c=
b
3

即b=3c，∴b2=9c2，即a2=10c2，
所以离心率e=
10
10

（2）因为B（0，3c），由几何关系可求得一条切线的斜率为2
2
，
所以切线方程为y-3c=2
2
x，即y=2
2
x+3c，
因为在轴上的截距为-
3
2
4
，所以c=1，
所求椭圆方程为：
x2
10
+
y2
9
=1
练习册系列答案
相关题目
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的左焦点为F椭圆与过原点的直线交于A，B两点，连接AF，BF，若|AB|=26，|BF|=10，cos∠ABF=
5
13
，则椭圆的离心率为（　　）
A．
5
13
B．
5
7
C．
13
17
D．
6
17
已知椭圆
x2
a2
+
y2
b2
=1上到点A（0，b）距离最远的点是B（0，-b），则椭圆的离心率的取值范围为（　　）
A．(0，
6
3
]		B．[
6
3
，1)		C．(0，
2
2
]		D．[
2
2
，1)
椭圆4x2+y2=4的准线方程是（　　）
A．y=±
4
3
3
x		B．x=±
4
3
3
y		C．y=±
4
3
3
D．x=
+-
4
3
3
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的两个焦点是F1（-c，0）、F2（c，0），M是椭圆上一点，且
F1M
•
F2M
=0，则离心率e的取值范围是 ______．
椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别是F1，F2，过F2作倾斜角为120°的直线与椭圆的一个交点为M，若MF1垂直于x轴，则椭圆的离心率为（　　）
A．
12-2
3
11
B．2-
3
C．2（2-
3
）		D．
3
3
“m=3”是“椭圆
x2
4
+
y2
m
=1焦距为2”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分又不必要条件
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为e=
2
2
，左、右焦点分别为F1、F2，点P的坐标为（2，
3
），且F2在线段PF1的中垂线上．
（Ⅰ）求椭圆C的方程；
（Ⅱ）如果圆E：（x-
1
2
）2+y2=r2被椭圆C所覆盖，求圆的半径r的最大值．
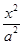已知双曲线－＝1(a＞0，b＞0)的一条渐近线方程是y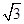＝x，它的一个焦点与抛物线y2＝16x的焦点相同，则双曲线的方程为________．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网