Question

（2008•上海模拟）函数f（x）=1-|2x-1|，则方程f（x）•2^x=1的实根的个数是

2个

．

Answer 1

分析：由f（x）•2^x=1可得，f（x）=(

1

2

)x，令g（x）=(

1

2

)x，分别作出函数f（x）与g（x）的图象，要求方程f（x）•2^x=1的实根的个数结合图象，只要判定函数f（x）与函数g（x）的交点个数即可

解答：解：函数f（x）=1-|2x-1|=

2-2x，x≥ 1 2 2x，x＜ 1 2

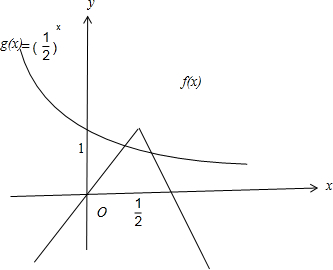
由f（x）•2^x=1可得，f（x）=(

1

2

)x，令g（x）=(

1

2

)x
分别作出函数f（x）与g（x）的图象，如图所示，结合图象可知函数f（x）与函数g（x）有2个交点
故答案为：2

点评：本题主要考查了方程的根的个数的判断，转化为分段函数与指数函数的交点个数的判断，解题的关键是准确作出函数的图象．