Question

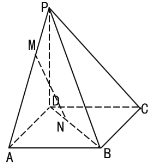
【题目】如图，四棱锥P-ABCD底面为正方形，PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点（不含端点），点N在线段BD上，且PM=DN.

（1）求证：直线MN∥平面PCD.

（2）若点M为线段PA的中点，求直线PB与平面AMN所成角的余弦值.

Answer 1

【答案】（1）详见解析；（2）

【解析】

（1）过点作交于，连接，通过相似证明得到平面平面，得到答案.

（2）以为 轴建立空间直角坐标系，计算得到平面的法向量为，利用夹角公式得到答案.

（1）如图所示：过点作交于，连接.

，

故，所以平面平面

故直线MN∥平面PCD

（2）由于 ，

以为 轴建立空间直角坐标系，

设,则

则 ,设平面的法向量为

根据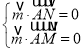 得到 故法向量

则向量 与 的夹角为,则，

则与平面夹角的余弦值为 .