题目内容
若不等式
+3y2≥
对任意的正数x,y恒成立,则正数k的取值范围为 .
| x2 |
| 4 |
| xy |
| k |
考点:函数恒成立问题
专题:综合题,不等式的解法及应用
分析:把不等式两边同时乘以
,然后利用基本不等式求得不等式左侧的最小值,由
小于等于该最小值求得k的取值范围.
| 1 |
| xy |
| 1 |
| k |
解答:
解:不等式
+3y2≥
对任意的正数x,y恒成立,
即
≥
对任意的正数x,y恒成立,
∵
≥
=
,
∴
≤
,∵k>0,∴k≥
.
∴正数k的取值范围是[
,+∞).
故答案为:[
,+∞).
| x2 |
| 4 |
| xy |
| k |
即
| ||
| xy |
| 1 |
| k |
∵
| ||
| xy |
2
| ||||
| xy |
| 3 |
∴
| 1 |
| k |
| 3 |
| ||
| 3 |
∴正数k的取值范围是[
| ||
| 3 |
故答案为:[
| ||
| 3 |
点评:本题考查恒成立问题,考查了分离变量法,训练了利用基本不等式求最值,是中档题.

练习册系列答案
相关题目
若x,y∈(0,2)且xy=2,使不等式a(2x+y)≥(2-x)(4-y)恒成立,则实数a的取值范围为( )
A、a≤
| ||
| B、a≤2 | ||
| C、a≥2 | ||
D、a≥
|
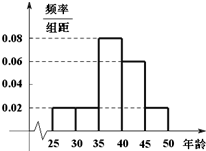 某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表.
某单位N名员工参加“社区低碳你我他”活动.他们的年龄在25岁至50岁之间.按年龄分组:第1组[25,30),第2组[30,35),第3组[35,40),第4组[40,45),第5组[45,50],得到的频率分布直方图如图所示.下表是年龄的频率分布表. 如图,茎叶图表示甲、乙两名篮球运动员在五场比赛中的得分,其中一个数字被污损,则甲的平均得分不超过乙的平均得分的概率为
如图,茎叶图表示甲、乙两名篮球运动员在五场比赛中的得分,其中一个数字被污损,则甲的平均得分不超过乙的平均得分的概率为