题目内容
已知函数f(x)＝2ax2＋2x－3.如果函数y＝f(x)在区间[－1,1]上有零点，则实数a的取值范围为______________．
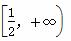解析 若a＝0，则f(x)＝2x－3，
f(x)＝0⇒x＝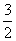
∉[－1,1]，不合题意，故a≠0.
下面就a≠0分两种情况讨论：
①当f(－1)·f(1)≤0时，f(x)在[－1,1]上有一个零点，即(2a－5)(2a－1)≤0，解得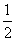
≤a≤
.
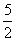②当f(－1)·f(1)>0时，f(x)在[－1,1]上有零点的条件是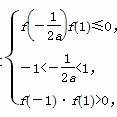
解得a>.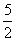
综上，实数a的取值范围为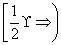
.
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
是偶函数，则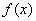
的递减区间是 .
，
，…，
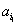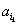}，定义X的“特征数列”为x1，x2，…，x100，其中
＝
＝…＝
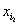＝1，其余项均为0.例如：子集{a2，a3}的“特征数列”为0,1,1,0,0，…，0.
若关于x的方程f2(x)－af(x)＝0恰有5个不同的实数解，则a的取值范围是________．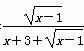
的最大值为________．
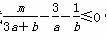恒成立，则m的最大值为________．
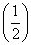|1－x|＋m的图象与x轴有公共点，则实数m的取值范围是________．
”是“函数
在
上是单调函数”的