题目内容
【题目】已知椭圆![]() ,右顶点
,右顶点![]() ,上顶点为B,左右焦点分别为
,上顶点为B,左右焦点分别为![]() ,且
,且![]() ,过点A作斜率为
,过点A作斜率为![]() 的直线l交椭圆于点D,交y轴于点E.
的直线l交椭圆于点D,交y轴于点E.
(1)求椭圆C的方程;
(2)设P为![]() 的中点,是否存在定点Q,对于任意的
的中点,是否存在定点Q,对于任意的![]() 都有
都有![]() ?若存在,求出点Q;若不存在,请说明理由.
?若存在,求出点Q;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() .
.
【解析】
(1)根据题中所给的条件,结合椭圆的性质,得到![]() ,
,![]() ,从而得到椭圆的方程;
,从而得到椭圆的方程;
(2)解法一,首先设直线直线![]() ,与椭圆方程
,与椭圆方程![]() 联立,利用韦达定理以及中点坐标公式得到P点坐标,从而有
联立,利用韦达定理以及中点坐标公式得到P点坐标,从而有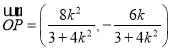 ,假设存在
,假设存在![]() 使得
使得![]() ,利用向量数量积等于零,从而求得结果.解法二,利用点差法
,利用向量数量积等于零,从而求得结果.解法二,利用点差法
(1)由题意得:![]()
![]() 在
在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,
,![]()
![]() 椭圆方程为
椭圆方程为![]()
(2)解法一:设直线![]()
令![]() ,则
,则![]() ,
,![]()
将*代入![]() 整理得
整理得![]()
设![]() ,则
,则![]() ,
,
![]() ,
,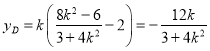
设![]() ,
,![]() 为
为![]() 的中点
的中点
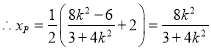 ,
,![]()

设存在![]() 使得
使得![]() ,则
,则![]() ,
,![]()
![]() ,即
,即![]() 对任意的
对任意的![]() 都成立
都成立
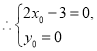 ,
,![]() ,
,![]() 存在
存在![]() 使得
使得![]()
解法二:设![]() ,
,![]() ,
,![]()
![]() ,①
,① ![]() ,②
,②
由①-②,得![]()
![]() 为
为![]() 中点,
中点,![]()
![]() ,
,![]()
![]() ,
,![]()
设存在![]() 使得
使得![]() ,
,
则![]() ,即
,即![]()
对任意![]() 都成立,即
都成立,即![]() ,
,![]() ,
,
![]() 存在
存在![]() 使得
使得![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某厂能够生产甲、乙两种产品,已知生产这两种产品每吨所需的煤、电以及每吨的产值分别是:
用煤(t) | 用电(kw) | 产值(千元) | |
甲种产品 | 70 | 20 | 80 |
乙种产品 | 30 | 50 | 110 |
如果该厂每月至多供煤560t,供电450kw,问如何安排生产,才能使该厂月产值最大?月产值是多少?