题目内容
在平面直角坐标系xOy 中, .
.
(1)求点 M,N的坐标;
(2)若角α,β的顶点都为坐标原点且始边都与x 轴的非负半轴重合,终边分别经过点 M,N,求tan(α+β)的值.
(本小题满分12分)
解:(1)∵ ,∴
,∴ ,….(2分)
,….(2分)
∴ ,
,
解得 ,
,
所以 ,
, ….(6分)
….(6分)
(2)由(1)可知 ,
,
∴tanα=6, ….(10分)
….(10分)
∴ =
= =
= ….(12分)
….(12分)
分析:(1)利用向量的数量积,求出θ的正弦函数与余弦函数值,即可求点 M,N的坐标;
(2)角α,β的顶点都为坐标原点且始边都与x 轴的非负半轴重合,终边分别经过点 M,N,利用任意角的三角函数的定义,求出α、β的正切函数值,利用两角和的正切函数直接求tan(α+β)的值.
点评:本小题主要考查了同角三角函数的关系、三角函数的定义、两角和正切公式,以及向量的有关知识.考查了运算能力.
解:(1)∵
 ,∴
,∴ ,….(2分)
,….(2分)∴
 ,
,解得
 ,
,
所以
 ,
, ….(6分)
….(6分)(2)由(1)可知
 ,
,
∴tanα=6,
 ….(10分)
….(10分)∴
 =
= =
= ….(12分)
….(12分)分析:(1)利用向量的数量积,求出θ的正弦函数与余弦函数值,即可求点 M,N的坐标;
(2)角α,β的顶点都为坐标原点且始边都与x 轴的非负半轴重合,终边分别经过点 M,N,利用任意角的三角函数的定义,求出α、β的正切函数值,利用两角和的正切函数直接求tan(α+β)的值.
点评:本小题主要考查了同角三角函数的关系、三角函数的定义、两角和正切公式,以及向量的有关知识.考查了运算能力.

练习册系列答案
相关题目
 在平面直角坐标系xOy中,已知点A(-1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.
在平面直角坐标系xOy中,已知点A(-1,1),P是动点,且三角形POA的三边所在直线的斜率满足kOP+kOA=kPA.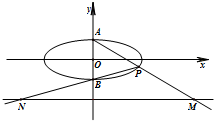 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: