题目内容
若x,y均为锐角,则( )
A、sinx+siny>2sin
| ||
B、sinx+siny<2sin
| ||
C、sinx+siny≤2sin
| ||
D、sinx+siny≥2sin
|
分析:利用和差化积公式写出sinx+siny=2sin
cos
,通过x,y均为锐角判断cos
的范围,然后得到选项.
| x+y |
| 2 |
| x-y |
| 2 |
| x-y |
| 2 |
解答:解:因为sinx+siny=2sin
cos
,x,y均为锐角,所以cos
∈[0,1],所以sinx+siny=2sin
cos
≤2sin
.
故选C
| x+y |
| 2 |
| x-y |
| 2 |
| x-y |
| 2 |
| x+y |
| 2 |
| x-y |
| 2 |
| x+y |
| 2 |
故选C
点评:本题考查三角函数的和差化积公式的应用,三角函数的解答范围,三角函数的值的范围,考查计算能力,公式的灵活运应能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
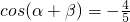 ,若设sinβ=x,cosα=y,则y关于x的函数关系为________.
,若设sinβ=x,cosα=y,则y关于x的函数关系为________.