题目内容
(理)已知α、β均为锐角,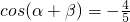 ,若设sinβ=x,cosα=y,则y关于x的函数关系为________.
,若设sinβ=x,cosα=y,则y关于x的函数关系为________.
y=
 +
+ x
x
分析:利用同角三角函数的基本关系求出cosβ= ,sinα=
,sinα= ,sin(α+β)=
,sin(α+β)= ,由y=cosα=
,由y=cosα=
cos[(α+β)-β],利用两角和差的余弦公式展开化简可得结果.
解答:∵α、β均为锐角,sinβ=x,cosα=y,∴cosβ= ,sinα=
,sinα= .
.
∵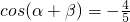 ,∴α+β 为钝角,故sin(α+β)=
,∴α+β 为钝角,故sin(α+β)= .
.
故y=cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=
 +
+ x,
x,
即 y=
 +
+ x,
x,
故答案为:y=
 +
+ x.
x.
点评:本题主要考查两角和差的余弦公式,同角三角函数的基本关系,角的变换是解题的关键.

 +
+ x
x分析:利用同角三角函数的基本关系求出cosβ=
 ,sinα=
,sinα= ,sin(α+β)=
,sin(α+β)= ,由y=cosα=
,由y=cosα=cos[(α+β)-β],利用两角和差的余弦公式展开化简可得结果.
解答:∵α、β均为锐角,sinβ=x,cosα=y,∴cosβ=
 ,sinα=
,sinα= .
.∵
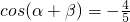 ,∴α+β 为钝角,故sin(α+β)=
,∴α+β 为钝角,故sin(α+β)= .
.故y=cosα=cos[(α+β)-β]=cos(α+β)cosβ+sin(α+β)sinβ=

 +
+ x,
x,即 y=

 +
+ x,
x,故答案为:y=

 +
+ x.
x.点评:本题主要考查两角和差的余弦公式,同角三角函数的基本关系,角的变换是解题的关键.

练习册系列答案
相关题目