题目内容
 如图,DA⊥平面ABC,BC⊥AC,E、F分别为BD与CD的中点,DA=AC=BC=2.
如图,DA⊥平面ABC,BC⊥AC,E、F分别为BD与CD的中点,DA=AC=BC=2.(1)证明:EF∥平面ABC;
(2)证明:EF⊥平面DAC;
(3)求三棱锥D-AEF的体积.
分析:(1)连接EF,证明EF∥BC,由线面平行的判定定理可证EF∥平面ABC;
(2)利用线面垂直的性质证明DA⊥BC,又BC⊥AC,由线面垂直的判定定理可证EF⊥平面DAC;
(3)先求三棱锥E-ADF的高与底面面积,再根据三棱柱的换底性,求三棱锥E-ADF的体积可得答案.
(2)利用线面垂直的性质证明DA⊥BC,又BC⊥AC,由线面垂直的判定定理可证EF⊥平面DAC;
(3)先求三棱锥E-ADF的高与底面面积,再根据三棱柱的换底性,求三棱锥E-ADF的体积可得答案.
解答:解:(1)证明:连接EF,
∵E,F为中点,∴EF∥BC,
∵EF?平面ABC,BC?平面ABC,
∴EF∥平面ABC;
(2)∵DA⊥面ABC,BC?平面ABC,∴DA⊥BC,
∵BC⊥AC,AD∩AC=A,∴BC⊥平面DAC
又∵EF∥BC,∴EF⊥平面DAC;
(3)连接AE,AF,由(2)知EF⊥平面ABC,
∴EF为三棱锥E-ADF的高,EF=
BC=1,
又AD=AC,AD⊥AC,F为CD的中点,
∴AF⊥CD,AF=
,DF=
,
∴VD-AEF=VE-ADF=
×S△ADF×EF=
×
×
×
×1=
.

∵E,F为中点,∴EF∥BC,
∵EF?平面ABC,BC?平面ABC,
∴EF∥平面ABC;
(2)∵DA⊥面ABC,BC?平面ABC,∴DA⊥BC,
∵BC⊥AC,AD∩AC=A,∴BC⊥平面DAC
又∵EF∥BC,∴EF⊥平面DAC;
(3)连接AE,AF,由(2)知EF⊥平面ABC,
∴EF为三棱锥E-ADF的高,EF=
| 1 |
| 2 |
又AD=AC,AD⊥AC,F为CD的中点,
∴AF⊥CD,AF=
| 2 |
| 2 |
∴VD-AEF=VE-ADF=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 3 |

点评:本题考查了线面平行的证明,线面垂直的证明,考查了三棱锥的体积计算,利用三棱锥的换底性求其体积是常用方法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2013•汕尾二模)如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.
(2013•汕尾二模)如图,四棱锥P-ABCD的底面ABCD为矩形,且PA=AD=1,AB=2,∠PAB=120°,∠PBC=90°.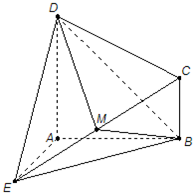 (2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.
(2008•深圳一模)如图所示的几何体ABCDE中,DA⊥平面EAB,CB∥DA,EA=DA=AB=2CB,EA⊥AB,M是EC的中点.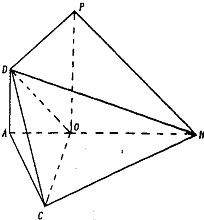 (2010•泰安二模)如图,在△ABC中,已知∠ABC=45°,O在AB上,且
(2010•泰安二模)如图,在△ABC中,已知∠ABC=45°,O在AB上,且
