题目内容
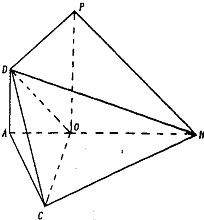（2010•泰安二模）如图，在△ABC中，已知∠ABC=45°，O在AB上，且OB=OC=| 2 |
| 3 |
| 1 |
| 2 |
（I）求证：PD⊥平面COD；
（II）求二面角A-BC-D的余弦值．
分析：（I）设OA=a，PO=OB=2a，DA=a，根据DA∥PO，且PO⊥平面ABC，得到DA⊥平面ABC，从而PD=DO=
a，则△PDO为直角三角形，即PD⊥DO，又CO⊥AB，PO⊥平面ABC，从而CO⊥平面PAB，根据线面垂直的性质可知CO⊥PD，最后根据线面垂直的判定定理可知PD⊥平面COD；
（II）过A作AE⊥BC，垂中为E，连接DE，根据二面角平面角的定义可知∠DEA为二面角A-BC-D的平面角，然后在△DEA中，求出此角的余弦值即可．
| 2 |
（II）过A作AE⊥BC，垂中为E，连接DE，根据二面角平面角的定义可知∠DEA为二面角A-BC-D的平面角，然后在△DEA中，求出此角的余弦值即可．
解答：
证明：（I）设OA=a，PO=OB=2a，DA=a，
由DA∥PO，且PO⊥平面ABC，
知DA⊥平面ABC．
从而PD=DO=
a，
在△PDO中∵PD=DO=
a，PO=2a∴△PDO为直角三角形，
故PD⊥DO（3分）
又∵OC=OB=2a，∠ABC=45°，∴CO⊥AB
又PO⊥平面ABC，∴CO⊥平面PAB，
故CO⊥PD．
∵CO与DO相交于点O．
∴PD⊥平面COD，（6分）
（II）∵DA⊥平面ABC
过A作AE⊥BC，垂中为E
连接DE，则∠DEA为二面角A-BC-D的平面角（8分）
在△ABC中，BC•AE=AB•OC
∴AE=
=
=
a
DE=
=
=
a
cos∠DEA=
=
=
所以二面角A-BC-D的余弦值为
．（12分）
证明：（I）设OA=a，PO=OB=2a，DA=a，由DA∥PO，且PO⊥平面ABC，
知DA⊥平面ABC．
从而PD=DO=
| 2 |
在△PDO中∵PD=DO=
| 2 |
故PD⊥DO（3分）
又∵OC=OB=2a，∠ABC=45°，∴CO⊥AB
又PO⊥平面ABC，∴CO⊥平面PAB，
故CO⊥PD．
∵CO与DO相交于点O．
∴PD⊥平面COD，（6分）
（II）∵DA⊥平面ABC
过A作AE⊥BC，垂中为E
连接DE，则∠DEA为二面角A-BC-D的平面角（8分）
在△ABC中，BC•AE=AB•OC
∴AE=
| AB•OC |
| BC |
| 3a•2a | ||
2
|
3
| ||
| 2 |
DE=
| DA2+AE2 |
a2+(
|
| ||
| 2 |
cos∠DEA=
| AE |
| DE |
3
| ||
|
3
| ||
| 11 |
所以二面角A-BC-D的余弦值为
3
| ||
| 11 |
点评：本小题主要考查空间线面关系、二面角的度量等知识，考查数形结合、化归与转化的数学思想方法，以及空间想象能力、推理论证能力和运算求解能力．
练习册系列答案
相关题目