题目内容
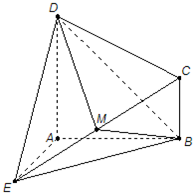（2008•深圳一模）如图所示的几何体ABCDE中，DA⊥平面EAB，CB∥DA，EA=DA=AB=2CB，EA⊥AB，M是EC的中点．（Ⅰ）求证：DM⊥EB；
（Ⅱ）求二面角M-BD-A的余弦值．
分析：（Ⅰ） 建立空间直角坐标系，利用坐标表示向量，借助于数量积为0，从而可证DM⊥EB；
（Ⅱ） 先求平面的法向量，利用法向量的夹角，求面面角．
（Ⅱ） 先求平面的法向量，利用法向量的夹角，求面面角．
解答：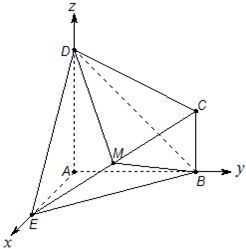
解：建立如图所示的空间直角坐标系，
并设EA=DA=AB=2CB=2，则
（Ⅰ）
=(1，1，-
)，
=(-2，2，0)，
所以
•
=0，从而得DM⊥EB；
（Ⅱ）设
=(x，y，z)是平面BDM的
法向量，则由
⊥
，
⊥
及
=(1，1，-
)，
=(0，2，-2)
得
⇒可以取
=(1，2，2)．
显然，
=(1，0，0)为平面ABD的法向量．
设二面角M-BD-A的平面角为θ，则此二面角的余弦值cosθ=|cos＜
，
＞|=
=
．
解：建立如图所示的空间直角坐标系，并设EA=DA=AB=2CB=2，则
（Ⅰ）
| DM |
| 3 |
| 2 |
| EB |
所以
| DM |
| EB |
（Ⅱ）设
| n1 |
法向量，则由
| n1 |
| DM |
| n1 |
| DB |
| DM |
| 3 |
| 2 |
| DB |
得
|
| n1 |
显然，
| n2 |
设二面角M-BD-A的平面角为θ，则此二面角的余弦值cosθ=|cos＜
| n1 |
| n2 |
|
| ||||
|
|
| 1 |
| 3 |
点评：本题以空间向量为手段，考查线线位置关系，考查面面角，关键是建立空间直角坐标系，用坐标表示向量．
练习册系列答案
相关题目