题目内容
已知: 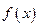 是定义在区间
是定义在区间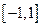 上的奇函数,且
上的奇函数,且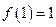 .若对于任意的
.若对于任意的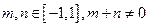 时,都有
时,都有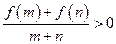 .
.
(1)解不等式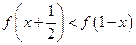 .
.
(2)若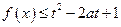 对所有
对所有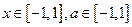 恒成立,求实数
恒成立,求实数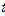 的取值范围
的取值范围
(1)令 则有
则有 ,即
,即 .
.
当 时,必有
时,必有

 在区间
在区间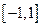 上是增函数
上是增函数
 解之
解之
所求解集为
(2)  在区间
在区间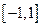 上是增函数,
上是增函数, 
又对于所有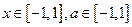 ,
,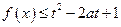 恒成立
恒成立 ,即
,即 在
在 时恒成立
时恒成立
记 ,则有
,则有 即
即
解之得, 或
或 或
或
 的取值范围是
的取值范围是
解析

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
题目内容
已知: 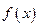 是定义在区间
是定义在区间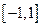 上的奇函数,且
上的奇函数,且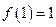 .若对于任意的
.若对于任意的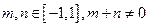 时,都有
时,都有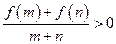 .
.
(1)解不等式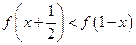 .
.
(2)若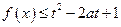 对所有
对所有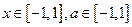 恒成立,求实数
恒成立,求实数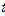 的取值范围
的取值范围
(1)令 则有
则有 ,即
,即 .
.
当 时,必有
时,必有

 在区间
在区间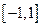 上是增函数
上是增函数
 解之
解之
所求解集为
(2)  在区间
在区间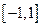 上是增函数,
上是增函数, 
又对于所有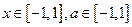 ,
,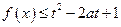 恒成立
恒成立 ,即
,即 在
在 时恒成立
时恒成立
记 ,则有
,则有 即
即
解之得, 或
或 或
或
 的取值范围是
的取值范围是
解析

 一本好题口算题卡系列答案
一本好题口算题卡系列答案