题目内容
直线l经过第一象限内的点M(a,b),与x、y轴的正半轴相交于点P、Q,求线段PQ的最小值,及取得最小值时直线的方程.
解:设l的方程为![]() +
+![]() =1(m、n>0),
=1(m、n>0),
则![]() =1,引进待定常数(a2α+b2α)(α∈R).
=1,引进待定常数(a2α+b2α)(α∈R).
由柯西不等式,得
(m2+n2)(a2α+b2α)≥(maα+nbα)2
=(maα+nbα)2·12
=(maα+nbα)2(![]() )2
)2
=[(maα+nbα)(![]() )]2
)]2
≥[(![]() )2]2=(
)2]2=(![]() )4.
)4.
当且仅当![]() 时,第一个不等式取等号;当且仅当
时,第一个不等式取等号;当且仅当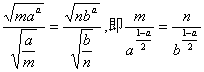 时,第二个不等式取等号.因此当且仅当两个等号同时成立时,
时,第二个不等式取等号.因此当且仅当两个等号同时成立时,
即α=![]() ,亦即α=
,亦即α=![]() 时,(m2+n2)(
时,(m2+n2)(![]() )≥(
)≥(![]() )4取等号.所以|PQ|=
)4取等号.所以|PQ|=![]() ,|PQ|min=
,|PQ|min=![]() .
.
此时k=-![]() =-
=-![]() ,
,
∴l:y-b=-![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若第一象限内的点A(x,y)落在经过点(6,-2)且方向向量为
=(3,-2)的直线l上,则t=log
y-log
x有( )
| a |
| 3 |
| 2 |
| 2 |
| 3 |
| A、最大值1 | ||
B、最大值
| ||
C、最小值
| ||
| D、最小值1 |