题目内容
若第一象限内的点A(x,y)落在经过点(6,-2)且方向向量为
=(3,-2)的直线l上,则t=log
y-log
x有( )
| a |
| 3 |
| 2 |
| 2 |
| 3 |
| A、最大值1 | ||
B、最大值
| ||
C、最小值
| ||
| D、最小值1 |
分析:由题意可得直线l的斜率为-
,点斜式求得直线l的 方程,利用基本不等式求得xy≤
,化简t 的解析式为
,由
≤1得到结论.
| 2 |
| 3 |
| 3 |
| 2 |
| log | xy
|
| log | xy
|
解答:解:由题意可得直线l的斜率为-
,故直线l的 方程为 y+2=-
(x-6),即 y=2-
x,
即 2x+3y=6.∵点A(x,y)在第一象限内,x,y>0,∴6=2x+3y≥2
,∴xy≤
.
∴t=log
y-log
x=log
y +log
=log
y +log
x=
≤1,
故t的最大值等于1,
故选 A.
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
即 2x+3y=6.∵点A(x,y)在第一象限内,x,y>0,∴6=2x+3y≥2
| 6xy |
| 3 |
| 2 |
∴t=log
| 3 |
| 2 |
| 2 |
| 3 |
| 3 |
| 2 |
| 2 |
| 3 |
| 1 |
| x |
| 3 |
| 2 |
| 3 |
| 2 |
| log | xy
|
故t的最大值等于1,
故选 A.
点评:本题考查用点斜式求直线方程,基本不等式的应用,对数的运算性质,判断 xy≤
,是解题的关键.
| 3 |
| 2 |

练习册系列答案
相关题目
若第一象限内的点A(x、y)落在经过点(6,-2)且具有方向向量
=(1,-
)的直线上,则log
x+log
y有( )
| e |
| 2 |
| 3 |
| 3 |
| 2 |
| 3 |
| 2 |
A、最大值
| ||
| B、最大值1 | ||
C、最小值
| ||
| D、最小值1 |
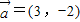 的直线l上,则t=
的直线l上,则t=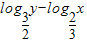 有( )
有( )

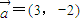 的直线l上,则t=
的直线l上,则t=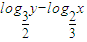 有( )
有( )
