题目内容

5．方程|x|+|y|=1表示的曲线是（　　）
A．B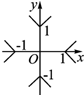．C．D．

分析 由曲线的方程可得，曲线关于两个坐标轴及原点都是对称的，故只要画出曲线在第一象限内的图象，在第一象限内，曲线是一条线段，y=x （0≤x≤1），则由对称性可得曲线的完整图象．

解答 解：方程|x|+|y|=1 即：x±y=1，或-x±y=1，（-1≤x≤1，且-1≤y≤1 ）
故方程|x|+|y|=1表示的曲线所围成的图形如图所示：曲线围成一个边长为$\sqrt{2}$的正方形，
故选：D．

点评 本题考查线段的方程特点，由曲线的方程研究曲线的对称性，体现了数形结合的数学思想．

练习册系列答案
相关题目
15．函数f（x）=sinx+cosx（x∈R）的图象向右平移了m个单位后，得到函数y=f′（x）的图象，其中m∈（0，2π），则m的值是$\frac{3π}{2}$．
16．将函数y=sin（x+$\frac{π}{6}$）的图象上各点的横坐标压缩为原来的$\frac{1}{2}$倍（纵坐标不变），所得函数在下面哪个区间单调递增（　　）
A．（-$\frac{π}{3}$，$\frac{π}{6}$）?B．（-$\frac{π}{2}$，$\frac{π}{2}$）?C．（-$\frac{π}{3}$，$\frac{π}{3}$）??D．（-$\frac{π}{6}$，$\frac{2π}{3}$）?
13．（文）不等式ax2+bx+2＞0的解集为（$-\frac{1}{2}，\frac{1}{3}$），则ab的值为（　　）
A．24B．-24C．12D．-12
20．已知平面直角坐标系xoy中，以O为极点，x轴的正半轴为极轴，建立极坐标系，曲线C1方程为ρ=2sinθ；C2的参数方程为$\left\{\begin{array}{l}x=-1+\frac{1}{2}t\\ y=\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t为参数）．
（Ⅰ）写出曲线C1的直角坐标方程和C2的普通方程；
（Ⅱ）设点P为曲线C1上的任意一点，求点P 到曲线C2距离的取值范围．
10．下列各图是正方体和正三棱柱（两底面为正三角形的直棱柱），G、N、M、H分别是顶点或所在棱的中点，则表示直线GH、MN是异面直线的图形有③．
17．已知函数f（x）=lnx+（x-b）2（b∈R）在区间$[{\frac{1}{2}，2}]$上存在单调递增区间，则实数b的取值范围是（　　）
A．$（{-∞，\frac{3}{2}}）$B．$（{-∞，\frac{9}{4}}）$C．（-∞，3）D．$（{-∞，\sqrt{2}}）$
14．已知tanα=$-\frac{4}{3}$，则$\frac{sinα+cosα}{sinα-cosα}$等于（　　）
A．$\frac{1}{7}$B．$-\frac{1}{7}$C．-7D．7
15．奇函数f（x）定义域是（t，2t+3），则t=（　　）
A．1B．0C．-1D．-2

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网