题目内容
已知函数 ,
, .
.
(Ⅰ)求函数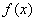 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的 ,都有
,都有 ,求
,求 的取值范围.
的取值范围.
解:(Ⅰ) 因为 ,
,
因为 ,
,
所以 .
.
所以

 .
.
令 ,解得
,解得 .
.
随着 的变化,
的变化, 和
和 的变化情况如下:
的变化情况如下:
|
|
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
| ↘ | ↗ | ↘ |
即 在
在 和
和 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
(Ⅱ) 因为对于任意的 ,都有
,都有 ,
,
即 ,
,
所以 .
.
设 .
.
因为 ,
,
又因为 ,
,
所以 .
.
所以 .
.
所以 在
在 上单调递增.
上单调递增.
所以 .
.
即 .
.

练习册系列答案
相关题目




 的各项均为正数,若
的各项均为正数,若 ,
, ,则
,则
 项和
项和
 天,为使投资的回报最多,你会选择哪种方案投资?
天,为使投资的回报最多,你会选择哪种方案投资? 中,
中, ,若
,若 为
为 的中点,则
的中点,则 的值为____;若点
的值为____;若点 为
为 边上的动点,点
边上的动点,点 是
是 边上的动点,且
边上的动点,且 ,
, ,
,  ,则
,则 的最大值为________ .
的最大值为________ . 是函数
是函数 的导函数,将
的导函数,将 和
和 的图像画在同一个平面直角坐标系中,下列各图 中不可能正确的是( )
的图像画在同一个平面直角坐标系中,下列各图 中不可能正确的是( )







 ”的否定是 .
”的否定是 . 的前n项和为
的前n项和为 ,
, ,则使得
,则使得 是定义在
是定义在 上的偶函数,且在区间
上的偶函数,且在区间 上是增函数.令
上是增函数.令 ,
, ,
, ,则( )
,则( ) B.
B. C.
C. D.
D.