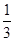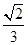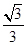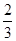题目内容
若{a,b,c}为空间的一组基底,则下列各项中,能构成基底的一组向量是( )
| A.a,a+b,a-b | B.b,a+b,a-b |
| C.c,a+b,a-b | D.a+b,a-b,a+2b |
C
解析试题分析:空间基底必须不共面. A中
A中 ,不可为基底;
,不可为基底;
B中 ,不可为基底;D中
,不可为基底;D中 ,不可为基底,故选C
,不可为基底,故选C
考点:空间向量的基本定理.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
在空间直角坐标系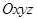 中,已知
中,已知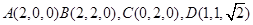 .若
.若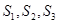 分别是三棱锥
分别是三棱锥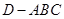 在
在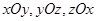 坐标平面上的正投影图形的面积,则( )
坐标平面上的正投影图形的面积,则( )
A.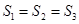 | B.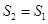 且 且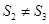 |
C.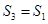 且 且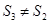 | D.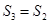 且 且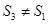 |
已知正四棱柱 中
中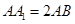 ,则
,则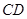 与平面
与平面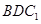 所成角的正弦值等于( )
所成角的正弦值等于( )
A.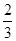 | B.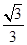 | C.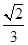 | D.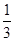 |
向量 =(2,4,x),
=(2,4,x),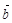 =(2,y,2),若|
=(2,y,2),若| |=6,且
|=6,且 ⊥
⊥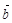 ,则x+y的值为( )
,则x+y的值为( )
| A.-3 | B.1 | C.-3或1 | D.3或1 |
若三点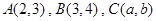 共线,则有( )
共线,则有( )
A.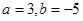 | B.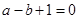 | C.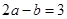 | D.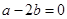 |
如图所示,在正方体ABCD-A1B1C1D1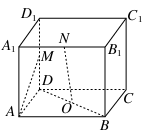
中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1上的动点,则直线NO、AM的位置关系是( )
| A.平行 | B.相交 |
| C.异面垂直 | D.异面不垂直 |
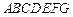 中,
中,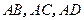 两两垂直,平面
两两垂直,平面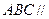 平面
平面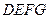 ,
,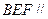 平面
平面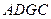 ,
, .
.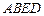 是正方形;
是正方形; 是否四点共面,并说明为什么?
是否四点共面,并说明为什么?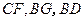 ,求证:
,求证: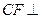 平面
平面 .
.
 内有一个三棱柱
内有一个三棱柱 ,三棱柱的 底面为圆柱
,三棱柱的 底面为圆柱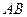 是圆
是圆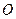 的直径。
的直径。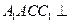 平面
平面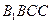 ;
;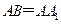 ,在圆
,在圆 柱
柱 。
。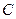 在圆周上运动时,求
在圆周上运动时,求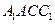 与平面
与平面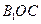 所成的角为
所成的角为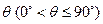 。当
。当
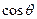 的值。
的值。