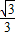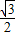题目内容
设函数f(x)的导数为f′(x),且f(x)=2x-f′(1)lnx+f′(2),则f′(2)的值是 .
分析:求出原函数的导函数,取x=1求得f′(1),代回导函数解析式,则f′(2)的值可求.
解答:解:由f(x)=2x-f′(1)lnx+f′(2),得
f′(x)=2xln2-
,取x=1得:f′(1)=2ln2-f′(1).
∴f′(1)=ln2.
则f′(x)=2xln2-
,
∴f′(2)=4ln2-
=
ln2.
故答案为:
ln2.
f′(x)=2xln2-
| f′(1) |
| x |
∴f′(1)=ln2.
则f′(x)=2xln2-
| ln2 |
| x |
∴f′(2)=4ln2-
| ln2 |
| 2 |
| 7 |
| 2 |
故答案为:
| 7 |
| 2 |
点评:本题考查了导数的运算,考查了基本初等函数的导数公式,是基础的计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
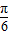 )cosx+sinx,则f′(
)cosx+sinx,则f′(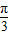 )=( )
)=( )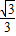
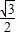
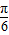 )cosx+sinx,则f′(
)cosx+sinx,则f′(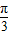 )=( )
)=( )