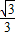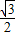题目内容
设函数f（x）的导数f′（x），且f（x）=f′（
）cosx+sinx，则f′（
）=（ ）
| π |
| 6 |
| π |
| 3 |
分析：对f（x）=f′（
）cosx+sinx两边求导，得f′（x）=-f′（
）sinx+cosx，令x=
可得f′（
），再令x=
即可求得f′（
）．
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
解答：解：由f（x）=f′（
）cosx+sinx，得f′（x）=-f′（
）sinx+cosx，
则f′（
）=-f′（
）•sin
+cos
，解得f′（
）=
，
所以f′（
）=-f′（
）sin
+cos
=-
×
+
=0，
故选B．
| π |
| 6 |
| π |
| 6 |
则f′（
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| ||
| 3 |
所以f′（
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| ||
| 3 |
| ||
| 2 |
| 1 |
| 2 |
故选B．
点评：本题考查导数的运算、三角函数值，考查学生对问题的分析解决能力．
练习册系列答案
相关题目
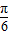）cosx+sinx，则f′（
）=（ ）
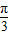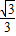
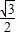
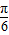）cosx+sinx，则f′（
）=（ ）
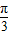