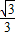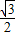题目内容
设函数f(x)的导数为f′(x),且f(x)=x2-f′(1)lnx,则f′(1)的值是分析:由导数计算公式求导,再令x=1得到关于f′(1)的方程,解方程可得所求值
解答:解:∵f(x)=x2-f′(1)lnx,
∴f′(x)=2x-f′(1)×
,
令x=1,解得f′(1)=1,
故答案为:.1
∴f′(x)=2x-f′(1)×
| 1 |
| x |
令x=1,解得f′(1)=1,
故答案为:.1
点评:本题考查导数运算规则,属于计算题,较简单

练习册系列答案
相关题目
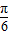 )cosx+sinx,则f′(
)cosx+sinx,则f′(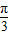 )=( )
)=( )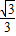
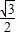
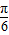 )cosx+sinx,则f′(
)cosx+sinx,则f′(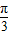 )=( )
)=( )