Question

已知A，B，P为椭圆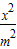+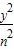=1（m，n＞0）上不同的三点，且A，B连线经过坐标原点，若直线PA，PB的斜率乘积k_PA•k_PB=-2，则该椭圆的离心率为    ．

Answer 1

【答案】分析：根据双曲线的对称性可知A，B关于原点对称，设出A，B和P的坐标，把A，B点坐标代入双曲线方程可求得直线PA和直线PB的斜率之积，进而求得m和n的关系，进而根据双曲线的离心率公式即可得出答案．
解答：解：根据双曲线的对称性可知A，B关于原点对称，
设A（x₁，y₁），B（-x₁，-y₁），P（x，y），
则-=1，有k_PA•k_PB=-=-2，∴=2．
∴e===．
故答案为：．
点评：本题主要考查了双曲线的简单性质．涉及了双曲线的对称性质，考查了学生对双曲线基础知识的全面掌握．