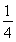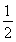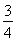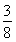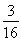题目内容
下表给出一个“三角形数阵”： 
，
，
，
……
已知每一列的数成等差数列；从第三行起，每一行的数成等比数列，每一行的公比都相等.记第i行第j列的数为aij(i≥j,i、j∈N*).
(1)求a83;
(2)试写出aij关于i、j的表达式；
(3)记第n行的和为An，求数列{An}的前m项和Bm的表达式.
解：(1)由题知，{ai1}成等差数列，
因为a11=,a21=,
所以，公差d=,a81=+(8-1)·=2.
又各行成等比数列，公比都相等，a31=,a32=
，
所以，每行的公比是q=
.
故a83=2×(
)2=
.
(2)由(1)知，ai1=
+(i-1)·
=
,
所以，aij=ai1·(
)j-1=
·(
)j-1=i(
)j+1.
(3)An=an1［1+
+(
)2+…+(
)n-1］=
［2-(
)n-1］=
-n(
)n+1,
Bm=
(1+2+…+m)-
(
+
+
+…+
).
设Tm=
+
+
+…+
, ①
则
Tm=
+
+
+…+
. ②
由①-②，得
Tm=
+
+…+
-
=1-
-
=1-
，
所以，Bm=
·
-(1-
)=
+
-1.
练习册系列答案
相关题目
下表给出一个“直角三角形数阵”：满足每一列成等差数列，从第三行起，每一行的数成等比数列，且每一行的公比相等，记第i行第j列的数为aij（i≥j，i，j∈N*）为
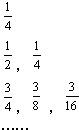下表给出一个“直角三角形数阵”满足每一列成等差数列，从第三行起，每一行成等比数列，且每一行的公比相等，记第i行，第j列的数为aij（i≥j，i，j∈N*），则a84等于（ ）
下表给出一个“直角三角形数阵”满足每一列成等差数列，从第三行起，每一行成等比数列，且每一行的公比相等，记第i行，第j列的数为aij（i≥j，i，j∈N*），则a84等于
