题目内容
在直角坐标系
中，曲线
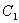的参数方程为
，（
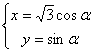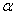为参数），以原点
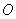为极点，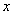
轴正半轴为极轴，建立极坐标系，曲线
的极坐标方程为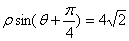
.
(1) 求曲线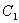的普通方程与曲线的直角坐标方程；
(2) 设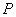
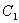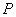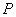为曲线上的动点，求点到上点的距离的最小值，并求此时点的坐标.
解：（1）由曲线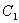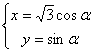： 得
两式两边平方相加得：
即曲线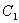的普通方程为：
由曲线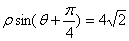：得：
即
，所以
即曲线的直角坐标方程为:
(2)由（1）知椭圆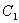与直线无公共点，椭圆上的点
到直线的距离为
所以当
时，
的最小值为
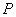，此时点的坐标为
练习册系列答案
相关题目
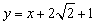总有公共点，则圆C的面积
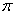(B) 有最小值2
， 则位于第10行的第8列的项等于 ，
在图中位于 ．（填第几行的第几列）
的离心率e为方程
的根，则满足条件的圆锥曲线的个数为( )
， 
，
的零点分别是
，
，
。则（ ）
＜
＜
B.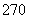 
人，其中一年级
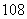人，二、三年级各
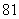人，现要利用抽样方法取
人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按一、二、三年级依次统一编号为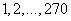
；使用系统抽样时，将学生统一随机编号
，
，若
，则
的最小值为
B．6 C．
D．
为随机变量，从棱长为1的正方体ABCD - A1B1C1D1的八个顶点中任取四个
点，当四点共面时，