题目内容
已知函数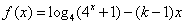 (
(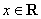 )为偶函数.
)为偶函数.
(1)求常数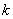 的值;
的值;
(2)当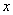 取何值时函数
取何值时函数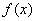 的值最小?并求出
的值最小?并求出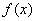 的最小值;
的最小值;
(3)设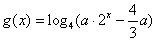 (
(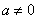 ),试根据实数
),试根据实数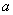 的取值,讨论函数
的取值,讨论函数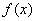 与
与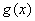 的图像的公共点个数.
的图像的公共点个数.
解:(1)∵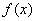 为偶函数,
为偶函数,
故 对所有
对所有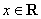 都成立,--
都成立,--  对所有
对所有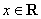 都成立,
都成立, 
(2)由(1)得 , 即
, 即 
 ,故当且仅当
,故当且仅当 时,-----10分
时,-----10分
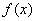 的最小值是
的最小值是 .
.
(3)解法1由方程 (
( )
)
可变形为 , 由②得
, 由②得 或
或 ,
,
由①得 ,令
,令 ,则
,则 ,或
,或
则 .
.
当 时,
时, 单调递增,∴
单调递增,∴ ,
,
∴ ,此时方程(
,此时方程( )有且只有一个解; -
)有且只有一个解; -
当 时,
时, ,
,
当 时方程(
时方程( )有且只有一个解;
)有且只有一个解;
当 时,方程(
时,方程( )有两解;
)有两解;
当 ,或
,或 时方程(
时方程( )无解.
)无解.
综上所述,当 时,函数
时,函数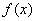 与
与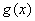 的图像有两个不同的公共点;
的图像有两个不同的公共点;
当 或
或 时,函数
时,函数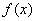 与
与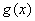 的图像有且只有一个公共点;
的图像有且只有一个公共点;
当 或
或 时,函数
时,函数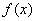 与
与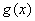 的图像没有公共点. -
的图像没有公共点. -
[解法2:  (
( )
) 

 --
-- 


 ,
, ,
,
 .
.

练习册系列答案
相关题目
 ,求随机变量
,求随机变量 }中,
}中, 为其前n项和,且
为其前n项和,且 ,当
,当 时,恒有
时,恒有 (
(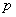
 为常数).
为常数). 时,求数列{
时,求数列{ ,数列
,数列 的前n项和为
的前n项和为 ,求证:
,求证: .
. 为地震时所散发出来的相对能量程度,则里氏震级量度
为地震时所散发出来的相对能量程度,则里氏震级量度 可定义为
可定义为 则日本9.0级地震和汶川8.0级地震的相对能量的比值
则日本9.0级地震和汶川8.0级地震的相对能量的比值 .(精确到整数)
.(精确到整数)  的三个内角满足
的三个内角满足 ,则△
,则△ ).
). B.0 C.
B.0 C. }的前n项和
}的前n项和 满足:
满足: ,且
,且 =1.那么
=1.那么 =( )
=( ) ,B=
,B= ,则集合
,则集合 ( )
( ) B.
B. C.
C. D.
D.