题目内容
已知数列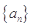 为等差数列且
为等差数列且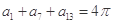 ,则
,则 的值为( )
的值为( )
A.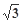 | B.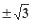 | C.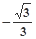 | D.—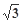 |
D
解析试题分析:由等差数列的性质, ,因为
,因为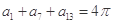 ,所以
,所以 ,
, ,
, ,
,
从而 ,
, =tan
=tan =tan(
=tan( )=tan
)=tan =-tan
=-tan =—
=—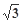 ,故选D。
,故选D。
考点:本题主要考查等差数列的性质,诱导公式的应用。
点评:小综合题,等差数列的性质是高考考查的重点内容之一,散见在教科书的例题、习题中,应注意总结汇总。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如果等差数列 中,
中,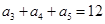 ,那么
,那么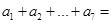 ( )
( )
| A.14 | B.21 | C.28 | D.35 |
已知两个正数a,b的等差中项为4,则a,b的等比中项的最大值为( )
| A.2 | B.4 | C.8 | D.16 |
若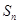 是等差数列
是等差数列 的前n项和,
的前n项和,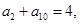 则
则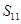 的值为( )
的值为( )
| A.12 | B.22 | C.18 | D.44 |
等差数列{an}的通项公式为an=2n+1,其前n项和为Sn,则{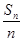 }前10项和为
}前10项和为
| A.120 | B.100 | C.75 | D.70 |
若 为等差数列
为等差数列 的前n项和,
的前n项和, ,
,  ,则
,则 与
与 的等比中项为( )
的等比中项为( )
A. | B. | C. | D. |
“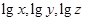 成等差数列”是“
成等差数列”是“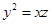 ”成立的( )
”成立的( )
| A.充分非必要条件 | B.必要非充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
等差数列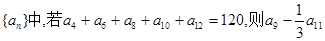 的值是( )
的值是( )
| A.14 | B.15 | C.16 | D.17 |
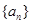 的前
的前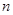 项和为
项和为 ,关于数列
,关于数列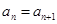 ;
;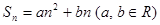 ,则数列
,则数列 ,则数列
,则数列