题目内容
如图，已知曲线C1∶y＝x2与C2∶y＝－（x－2）2，直线l与C1、C2都相切，求直线l的方程。
答案：
解析：
解析：
| 解：设l与C1相切于点P（x1、x12），与C2相切于点
Q（x2，－（x2－2）2）。 对于C2 : ＝2x1（x－x1），即y＝2x1x－x13。① 对于C2∶ ＋（x2－2）2＝－2（x2－2）（x－x2），即y＝－2（x2－2）＋x22－4。② ∵ 两切线重合， ∴ 2x1＝－2（x2－2）且－x12＝x22－4。 解得x1＝0，x2＝2或x1＝2，x2＝0。
∴ l的方程为y＝0或y＝4x－4。
|
＝2x，则与C1相切于点P的切线方程为y－x12
＝－2（x－2）则与C2相切于点Q的切线方程为y
练习册系列答案
相关题目
如图，已知曲线C1：y=x3（x≥0）与曲线C2：y=-2x3+3x（x≥0）交于O，A，直线x=t（0＜t＜1）与曲线C1，C2分别交于B，D．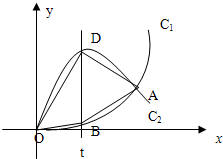
如图，已知曲线C1：y=x3（x≥0）与曲线C2：y=-2x3+3x（x≥0）交于O，A，直线x=
（2007•广州一模）如图，已知曲线C1：y=x2与曲线C2：y=-x2+2ax（a＞1）交于点O，A，直线x=t（0＜t≤1）与曲线C1，C2分别相交于点D，B，连结OD，DA，AB，OB．
（2009•黄冈模拟）如图，已知曲线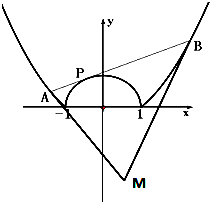
如图，已知曲线C1：x2+y2=1（|x|＜1），C2：x2=8y+1（|x|≥1），动直线l与C1相切，与C2相交于A，B两点，曲线C2在A，B处的切线相交于点M．