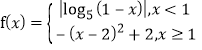Question

【题目】已知函数 .

(1)若，求的最小值；

(2)若,求的单调区间；

(3)试比较与的大小,并证明你的结论.

Answer 1

【答案】(1)0；(2)见解析；(3)见证明.

【解析】

（1）a＝1时，f（x）＝|x﹣1|﹣lnx，将绝对值符号化去，分类讨论，再求导函数，即可确定函数的单调区间，进而可得f（x）的最小值；

（2）将绝对值符号化去，分类讨论，再求导函数，即可确定函数的单调区间；

（3）由（1）可知，lnx≤x﹣1，从而，令x＝n2，可得，再进行叠加，利用放缩法，即可证得结论成立．

(1) 当时,， 在上是递增.

当时,,.在上是递减.

故时, 的增区间为,减区间为,.

(2) ①若,

当时,,,则在区间上是递增的;

当时,,,则在区间上是递减的

②若,

当时，，

,

则在上是递增的, 在上是递减的;

当时, ,

在区间(0,a)上是递减的,而在x=a处有意义;

则在区间上是递增的,在区间(0,1)上是递减的

综上: 当时, 的递增区间是,递减区间是(0,a);

当,的递增区间是,递减区间是(0,1)

(3)由(1)可知,当a=1,x时,有

即,

则有+

,

故：+ .