题目内容
直角三角形ABC的两条直角边BC=1，AC=| 3 |
| OP |
| OQ |
分析：设AB的中点为E，则由题意可得OE=
AB=1，
=
（
+
），利用两个向量的加减法的法则，以及其几何意义化简
•
为
•
，故当
=2
时，
•
最大为 2
2，从而得到结果．
| 1 |
| 2 |
| OE |
| 1 |
| 2 |
| OA |
| OB |
| OP |
| OQ |
| OE |
| OC |
| OC |
| OE |
| OP |
| OQ |
| OE |
解答：解：设AB的中点为E，则由题意可得OE=
AB=1，
=
（
+
），
∵
=
+
=
+
，
=
+
=
+
，
∴
•
=（
+
）•（
+
）=
•
+
•
+
•
+
•
．
由于OA⊥OB，AC⊥BC，∴
•
=0，
•
=0，
∴
•
=
•
+
•
=
•(
-
)+
•(
-
)=
•
-
•
+
•
-
•
=
•
+
•
=
（
+
）•
=
•
，
故当
与
共线时，即
=2
时，
•
最大为 2
2=2×1=2，
故选B．
| 1 |
| 2 |
| OE |
| 1 |
| 2 |
| OA |
| OB |
∵
| OP |
| OB |
| BP |
| OB |
| ||
| 2 |
| OQ |
| OA |
| AQ |
| OA |
| ||
| 2 |
∴
| OP |
| OQ |
| OB |
| ||
| 2 |
| OA |
| ||
| 2 |
| OA |
| OB |
| OB |
| ||
| 2 |
| OA |
| ||
| 2 |
| 1 |
| 4 |
| BC |
| AC |
由于OA⊥OB，AC⊥BC，∴
| OA |
| OB |
| 1 |
| 4 |
| BC |
| AC |
∴
| OP |
| OQ |
| OB |
| ||
| 2 |
| OA |
| ||
| 2 |
| 1 |
| 2 |
| OB |
| OC |
| OA |
| 1 |
| 2 |
| OA |
| OC |
| OB |
| 1 |
| 2 |
| OB |
| OC |
| 1 |
| 2 |
| OA |
| OB |
| 1 |
| 2 |
| OA |
| OC |
| 1 |
| 2 |
| OA |
| OB |
=
| 1 |
| 2 |
| OB |
| OC |
| 1 |
| 2 |
| OA |
| OC |
| 1 |
| 2 |
| OA |
| OB |
| OC |
| OE |
| OC |
故当
| OE |
| OC |
| OC |
| OE |
| OP |
| OQ |
| OE |
故选B．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量的数量积的运算，属于中档题．
练习册系列答案
相关题目
如图，AC、BC分别是直角三角形ABC的两条直角边，且AC=3，BC=4，以AC为直径作圆与斜边AB交于D，则BD=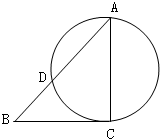
．A，B两点分别在x轴、y轴的正半轴（含原点）上滑动，P，Q分别为AC，BC的中点．则
的最大值是（ ）
