题目内容
如图，已知PA是圆O的切线，切点为A，PO交圆O于B，C两点，PA=
，PB=1，则圆O的半径为______，∠C=______．
| 3 |
由圆的切割线定理可得 PA2=PB?PC，即 3=1×PC，∴PC=3，故 BC=2，半径OB=1．
∵点O在BC上，即BC是圆O的直径，∴∠ABC=90°．
由弦切角定理，得∠PAB=∠C，∠PAC=90°+∠C．
∴△PAC中，根据正弦定理，得
=
，即
=
，解得tanC=
，
∵∠C是锐角，∴∠C=
．
故答案为：1、
．
∵点O在BC上，即BC是圆O的直径，∴∠ABC=90°．
由弦切角定理，得∠PAB=∠C，∠PAC=90°+∠C．
∴△PAC中，根据正弦定理，得
| PA |
| sinC |
| PC |
| sin∠PAC |
| ||
| sinC |
| 3 | ||
sin(
|
| ||
| 3 |
∵∠C是锐角，∴∠C=
| π |
| 6 |
故答案为：1、
| π |
| 6 |
练习册系列答案
名师金手指领衔课时系列答案
相关题目
15、（几何证明选讲）如图，已知PA是圆O的切线，切点为A，直线PO交圆O于B，C两点，AC=2，∠PAB=120°，则圆O的面积为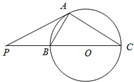
如图，已知PA是圆O的切线，切点为A，PO交圆O于B，C两点，
如图，已知PA是圆O的切线，切点为A，AC是圆O的直径，PC与圆O交于点B，PA=4，圆O的半径是
（几何证明选讲选做题）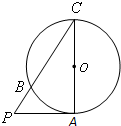
（2010•深圳模拟）（《几何证明选讲》选做题）如图：已知PA是圆O的切线，切点为A，