题目内容
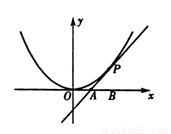
如图,已知直线l过坐标原点,抛物线C的顶点在原点,焦点在x轴的正半轴上,若点A(-1,0)和点B(0,8)关于直线l的对称点都在C上,求直线l和抛物线C的方程.
解:设抛物线C的方程为y2=2px(p>0).
由于x轴、y轴不是所求的直线,故可设直线l的方程为y=kx(k≠0).
设A′(x1,y1)、B′(x2,y2)分别为A、B关于l的对称点,
因而AA′⊥l,且AA′的中点(![]() ,
,![]() )在直线l上.
)在直线l上.
由此得方程组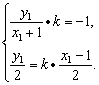
解得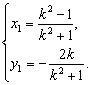 ①
①
同理得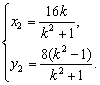 ②
②
又A′、B′均在抛物线y2=2px(p>0)上,
将①代入,得(-![]() )2=2p·
)2=2p·![]() .
.
整理得k≠±1且p=![]() . ③
. ③
同理,由②代入,得[![]() ]2=2p·
]2=2p·![]() .
.
整理得p=![]() . ④
. ④
∴![]() =
=![]() .
.
解得k1=![]() ,k2=
,k2=![]() .
.
但当k=![]() 时,由④知p<0,故应舍去.
时,由④知p<0,故应舍去.
∴k=![]() .代入③,求得p=
.代入③,求得p=![]() .
.
∴直线方程为y=![]() x,
x,
抛物线方程为y2=![]() x.
x.
点评:(1)本题是一道直线与抛物线的方程求解的综合题,考查的是基本概念和性质.这是解析几何的基本思想方法.
(2)对称问题主要是平分、垂直的问题.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
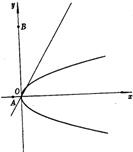 已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.
已知直线l过坐标原点,抛物线C顶点在原点,焦点在x轴正半轴上.若点A(-1,0)和点B(0,8)关于l的对称点都在C上,求直线l和抛物线C的方程.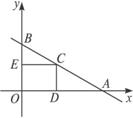
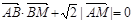 ,求点M的轨迹C;(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间)试求△OBE与△OBF面积之比的取值范围.
,求点M的轨迹C;(2)若过点B的直线l′(斜率不等于零)与(1)中的轨迹C交于不同的两点E,F(E在B,F之间)试求△OBE与△OBF面积之比的取值范围.