题目内容
已知正方形四个顶点分别为O(0,0),A(1,0),B(1,1),C(0,1),曲线y=x2(x≥0)与x轴,直线x=1构成区域M,现将一个质点随机地投入正方形中,则质点落在区域M内的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:欲求图象恒在x轴上方的概率,则可建立关于a,b的直角坐标系,画出关于a和b的平面区域,再根据几何概型概率公式结合定积分求面积的方法易求解.
解答: 解:本题是几何概型问题,
解:本题是几何概型问题,
曲线y=x2(x≥0)与x轴,直线x=1构成区域M,其面积为:
S1=线
x2dx=
x3
=
,
∴“质点落在区域M内的概率”事件对应的区域面积为
,
则质点落在区域M内的概率是
=
.
故选C.
 解:本题是几何概型问题,
解:本题是几何概型问题,曲线y=x2(x≥0)与x轴,直线x=1构成区域M,其面积为:
S1=线
| ∫ | 1 0 |
| 1 |
| 3 |
| | | 1 0 |
| 1 |
| 3 |
∴“质点落在区域M内的概率”事件对应的区域面积为
| 1 |
| 3 |
则质点落在区域M内的概率是
| ||
| 1 |
| 1 |
| 3 |
故选C.
点评:本题综合考查了平面直角坐标系,几何概型,及定积分在求面积中的应用,是一道综合性比较强的题目,考生容易在建立直角坐标系中出错,可多参考本题的做法.

练习册系列答案
相关题目
 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数 图象上,且正方形的一个顶点为
图象上,且正方形的一个顶点为 .
. ,
, 的值;
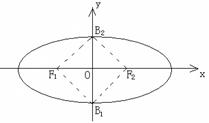
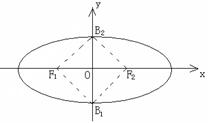
的值; 的两焦点
的两焦点 和短轴的两端点
和短轴的两端点 正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为 .
.
 的任一条直径,求
的任一条直径,求 的
的 底面是正方形且四个顶点
底面是正方形且四个顶点 在球
在球 的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点
的同一个大圆(球面被过球心的平面截得的圆叫做大圆)上,点 在球面上且
在球面上且 面
面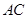 ,且已知
,且已知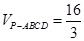 。
。 为
为 中点,求异面直线
中点,求异面直线 与
与 所成角的余弦值。
所成角的余弦值。
 的中心在原点,四个顶点都在函数
的中心在原点,四个顶点都在函数 图象上,且正方形的一个顶点为
图象上,且正方形的一个顶点为 .
. ,
, 的值;
的值; 的两焦点
的两焦点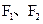 和短轴的两端点
和短轴的两端点 正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为
正好是一正方形的四个顶点,且焦点到椭圆上一点的最近距离为 .
.
 的任一条直径,求
的任一条直径,求 的
的