题目内容
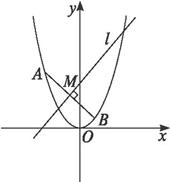
若抛物线y=2x2上的两点A(x1,y1)、B(x2,y2)关于直线l:y=x+m对称,且x1x2=-
,求实数m的值.
思路解析：关于直线对称,则满足①与直线垂直，②中点在直线上. 解：如图所示，∵A、B两点关于直线l对称， ∴AB⊥l且AB中点M（x0，y0）在直线l上. ∴x1+x2=- 由x1x2=- 又x0= 即点M为(- ∴m=
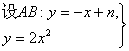
2x2+x-n=0,
,x1x2=-
.
得n=1,
=-
,y0=-x0+n=
+1=
,
,
),由点M在直线l上,得
=-
+m.
.
练习册系列答案
课课练与单元测试系列答案
世纪金榜小博士单元期末一卷通系列答案
单元测试AB卷台海出版社系列答案
黄冈新思维培优考王单元加期末卷系列答案
名校名师夺冠金卷系列答案
小学英语课时练系列答案
培优新帮手系列答案
课堂作业广西教育出版社系列答案
相关题目
,求m的值.
,则实数m的值为________________.
,则M等于( )
B.
C.-3 D.3