题目内容
如果在数列{an}中,a1=1,对任何正整数n,等式an+1=| n+2 | n |
分析:由已知中数列{an}中,a1=1,对任何正整数n,等式an+1=
an都成立,我们分别令n=2,3,4,…,n则可得an=
•
•
•…•
•
,约分整理后,即可得到数列{an}的通项公式.
| n+2 |
| n |
| 3 |
| 1 |
| 4 |
| 2 |
| 5 |
| 3 |
| n |
| n-2 |
| n+1 |
| n-1 |
解答:解:∵a1=1,an+1=
an,
∴a2=
,
a3=
•
,
a4=
•
•
,
…
an=
•
•
•…•
=
故答案为an=
| n+2 |
| n |
∴a2=
| 3 |
| 1 |
a3=
| 3 |
| 1 |
| 4 |
| 2 |
a4=
| 3 |
| 1 |
| 4 |
| 2 |
| 5 |
| 3 |
…
an=
| 3 |
| 1 |
| 4 |
| 2 |
| 5 |
| 3 |
| n+1 |
| n-1 |
| n(n+1) |
| 2 |
故答案为an=
| n(n+1) |
| 2 |
点评:本题考查的知识点是数列的递推公式,其中根据数列{an}中,a1=1,对任何正整数n,等式an+1=
an都成立,选择采用累乘法进行求解,是解答本题的关键.
| n+2 |
| n |

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
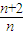 an都成立,那么数列{an}的通项公式为 .
an都成立,那么数列{an}的通项公式为 . 的值等于 .
的值等于 .