题目内容
如果在数列{an}中，a1=1，对任何正整数n，等式nan+1=（n+2）an都成立，那么
的值等于 ．
【答案】分析：由题设条件知，需要先求出通项an，由对任何正整数n，等式nan+1=（n+2）an都成立知，可用累乘法求出通项，再代入求极限即可
解答：解：由任何正整数n，等式nan+1=（n+2）an都成立知
即
=
故有
=
=
=
又a1=1，故an=
由
=
=
=
故答案为
点评：本题考查数列的极限，由题设中所给的递推关系求出通项再求其极限，数列的极限是数列中一类比较重要的题型，其特征是数列是无限的．
解答：解：由任何正整数n，等式nan+1=（n+2）an都成立知
即=故有
===又a1=1，故an=
由
===故答案为
点评：本题考查数列的极限，由题设中所给的递推关系求出通项再求其极限，数列的极限是数列中一类比较重要的题型，其特征是数列是无限的．
练习册系列答案
相关题目
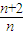an都成立，那么数列{an}的通项公式为 ．