题目内容
已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，边长为2a，AD＝DE＝2AB，F为CD的中点．
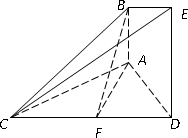
(1)求证：AF∥平面BCE；
(2)求证：平面BCE⊥平面CDE；
(3)求直线BF和平面BCE所成角的正弦值．
答案：
解析：
解析：
|
解：依题意，建立如图所示的坐标系 ∵
(1)证明 ∵ ∴ (2)证明：∵ ∴ ∴ (3)解：设平面 ∴直线 |
，则
．
为
的中点，∴
．
，
，
平面
，
平面
4分
，
，∴
．
平面
，又
平面
平面CDE 8分
的法向量为
，由
可得：
，取
．又
，设
和平面
所成的角为
，则
．
13分
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
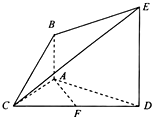如图，已知AB⊥平面ACD，DE∥AB，△ACD是正三角形，AD=DE=2AB，且F是CD的中点．
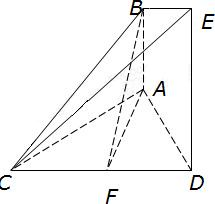如图，已知AB⊥平面ACD，DE⊥平面ACD，△ACD为等边三角形，AD=DE=2AB，F为CD的中点．
（2012•许昌二模）如图，已知AB⊥平面ACD，DE∥AB，△ACD是正三角形，AD=DE=2AB，且F是CD的中点．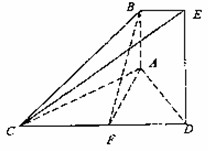
如图，已知AB⊥平面ACD，DE⊥平面ACD，△ABC为等边三角形，AD=DE=2AB，F为CD的中点．