题目内容
 如图,BC=2,原点O是BC的中点,点A的坐标为(
如图,BC=2,原点O是BC的中点,点A的坐标为(
| ||
| 2 |
| 1 |
| 2 |
(1)求向量
| CD |
(2)求异面直线AD与BC所成角的余弦值.
分析:(1)过D作DE⊥BC于E,求出D 的坐标,然后求向量
的坐标;
(2)求出向量
=(-
,-1,
),
=(0,2,0),
利用cos<
,
>=
,求异面直线AD与BC所成角的余弦值.
| CD |
(2)求出向量
| AD |
| ||
| 2 |
| ||
| 2 |
| BC |
利用cos<
| AD |
| BC |
| ||||
|
|
解答:解:(1)过D作DE⊥BC于E,则DE=CD•sin30°=
,OE=OB-BDcos60°=1-
=
,
∴D的坐标为(0,-
,
),
又∵C(0,1,0),
∴
=(0,-
,
)
(2)依题设有A点坐标为A(
,
,0),
∴
=(-
,-1,
),
=(0,2,0)
则cos<
,
>=
=-
,
故异面直线AD与BC所成角的余弦值为
.
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴D的坐标为(0,-
| 1 |
| 2 |
| ||
| 2 |
又∵C(0,1,0),
∴
| CD |
| 3 |
| 2 |
| ||
| 2 |
(2)依题设有A点坐标为A(
| ||
| 2 |
| 1 |
| 2 |
∴
| AD |
| ||
| 2 |
| ||
| 2 |
| BC |
则cos<
| AD |
| BC |
| ||||
|
|
| ||
| 5 |
故异面直线AD与BC所成角的余弦值为
| ||
| 5 |
点评:本题考查用空间向量求直线间的夹角、距离,空间直角坐标系,考查计算能力,逻辑思维能力,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
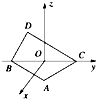 如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(
如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是( 如图,BC=2,原点O是BC的中点,点A的坐标为
如图,BC=2,原点O是BC的中点,点A的坐标为 ,点D在平面yoz上,且∠BDC=90°,∠DCB=30°.
,点D在平面yoz上,且∠BDC=90°,∠DCB=30°. 的坐标;
的坐标; ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°. 的坐标
的坐标 的夹角的大小.
的夹角的大小.