题目内容
 如图,BC=2,原点O是BC的中点,点A的坐标为 (
如图,BC=2,原点O是BC的中点,点A的坐标为 (
| ||
| 2 |
| 1 |
| 2 |
(1)求向量
| OD |
(2)求向量
| AD |
| BC |
分析:(1)由∠BDC=90°,∠DCB=30°,在平面yOz上,过点D作y轴的垂线,垂足为E,得DO=OB=OC=1,可得D的坐标,从而可得
的坐标;
(2)求出
和
的坐标,利用向量的夹角公式,即可求
和
的夹角的大小.
| OD |
(2)求出
| AD |
| BC |
| AD |
| BC |
解答:解:(1)由∠BDC=90°,∠DCB=30°,在平面yOz上,过点D作y轴的垂线,垂足为E,得DO=OB=OC=1,
所以D(0,-
,
),即
的坐标为(0,-
,
)(6分)
(2)∵D(0,-
,
),A(
,
,0),B(0,-1,0),C(0,1,0)
∴
=(-
,-1,
),
=(0,2,0),
∴cos<
,
>=
=
=-
(12分)
所以D(0,-
| 1 |
| 2 |
| ||
| 2 |
| OD |
| 1 |
| 2 |
| ||
| 2 |
(2)∵D(0,-
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
∴
| AD |
| ||
| 2 |
| ||
| 2 |
| BC |
∴cos<
| AD |
| BC |
| ||||
|
|
| -2 | ||||||
|
| ||
| 5 |
点评:本题考查向量知识的运用,考查向量的夹角公式,考查学生的计算能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
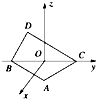 如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是(
如图所示,在空间直角坐标系中BC=2,原点O是BC的中点,点A的坐标是( 如图,BC=2,原点O是BC的中点,点A的坐标为
如图,BC=2,原点O是BC的中点,点A的坐标为 ,点D在平面yoz上,且∠BDC=90°,∠DCB=30°.
,点D在平面yoz上,且∠BDC=90°,∠DCB=30°. 的坐标;
的坐标; ,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°.
,0),点D在平面yOz上,且∠BDC=90°,∠DCB=30°. 的坐标
的坐标 的夹角的大小.
的夹角的大小.